円周上の点がつくる三角形（1）

円周上に点をとる作業を進めてきたが、これに関連した問題。

円周上にランダムに3点をとり、これらを頂点とする三角形をつくるとき、これが鋭角三角形、直角三角形、鈍角三角形となる条件について調べてみた。

原点を中心とする半径1の単位円において、座標(1,0)に点Aを固定し、上半円の適当な位置に点Bをとる。このとき、第3点目の点Cのとり方によって、鋭角三角形（青色）、直角三角形（赤色）、鈍角三角形（緑色）のいずれもつくることができる。

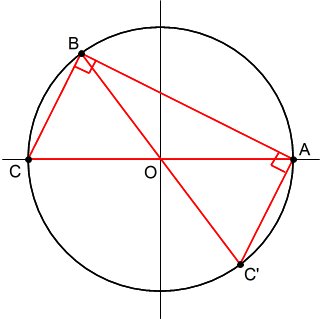
初めに、2点A,Bを固定したときの、直角三角形になる場合を考えると、

∠ABCと∠BACが直角になる2種類の直角三角形をつくることができる。ACまたはBCが中心Oを通る（直径になる）ように、点Cをとればよい。

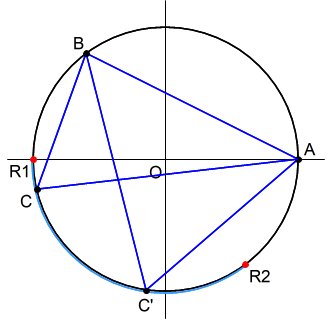
そして、鋭角三角形または鈍角三角形となる条件は、このポイントが分岐点となる（この分岐点をR1､R2とする）。

2点A,Bを固定したときの、鋭角三角形は、上記の分岐点R1とR2を端点とする弧（半円より小さいもの、弧ABを含まない側）の上に、点Cをとればよい。

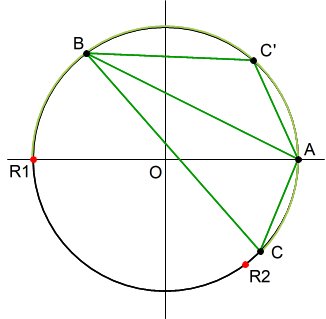
逆に、鈍角三角形は、弧R1BAR2の上に、点Cをとればよいということになる。

点Aは固定したまま、点Bの位置を上半円の円周上で動かした場合、鋭角三角形と鈍角三角形の現れやすさを調べてみよう。

点Bを第1象限にとると、分岐点R2（直角三角形を形成する点）は第3象限に現れる。なお、R1は点Aを固定しているのでつねに定位置（座標(-1,0)）にある。

点Bが点Aに近づくにしたがって、この青色のエリアは狭くなり、点BがR1に近づくにしたがって、青色のエリアは下半円全体に広がっていく。

そして、点Cが青色のエリアにあれば鋭角三角形、緑色のエリア（点A､Bをのぞく）にあれば鈍角三角形となることが分かる。

したがって、円周上にランダムにとった3点で作られる三角形が鋭角三角形になる確率を求めることは、弧R1R2の長さ（＝弧ABの長さ）の平均が全円周に対してどれくらいの割合になるかを調べることと同じである。

円周上にランダムに2点をとったときの弧の長さの平均はすでに調べた通り、π/2 であった。

したがって、鋭角三角形になる確率は、(π/2)÷2π＝1/4　となる。

ちなみに、鈍角三角形になる確率は、3/4 であり、直角三角形になる確率は、0（極めて珍しいこと）となる。