弦の長さとベルトランのパラドックス

これまでの「ランダムに引いた弦の長さ」の考察から「ベルトランのパラドックス」の確率を検証したい。

初めに、ベルトランのパラドックスについておさらいしておく。

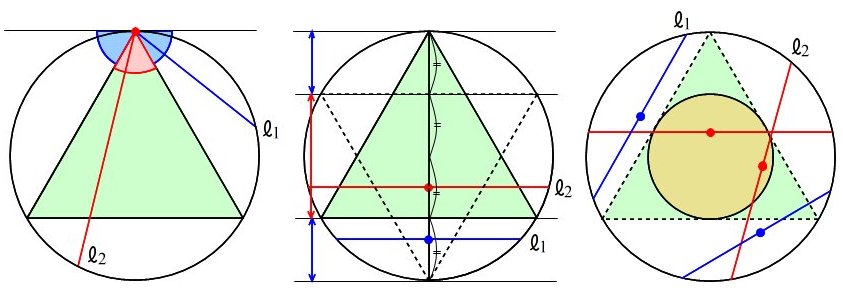
半径が1の円にランダムに引いた弦の長さが√3以上になる確率について、

（1）円周上にランダムに2点をとって弦をつくったとき、確率は、1/3

（2）直径上にランダムな1点をとって弦をつくったとき、確率は、1/2

（3）円の内部にランダムな1点をとって弦をつくったとき、確率は、1/4

一方、「円の中にランダムに引いた弦の長さ」を調べてきた方法を整理すると、

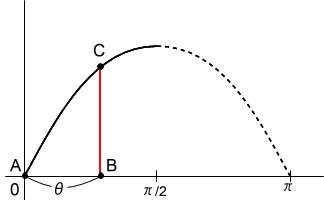
（1）円周上に適当なに2点をとったとき（方法①②③）、弦の長さの変化は y=2sinθに従い、平均値は4/π（約1.27）

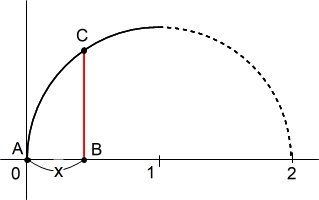
（2）直径上に適当な1点をとったとき（方法④）、弦の長さの変化は y＝2√(2x-x^2) に従い、平均値はπ/2（約1.57）

（3）円の内部に適当な1点をとったとき（方法⑤）、弦の長さの変化は y＝2√(1-(t/π))に従い、平均値は4/3（約1.33）　（ tは打点を円周上にもつ円の面積に相等） 

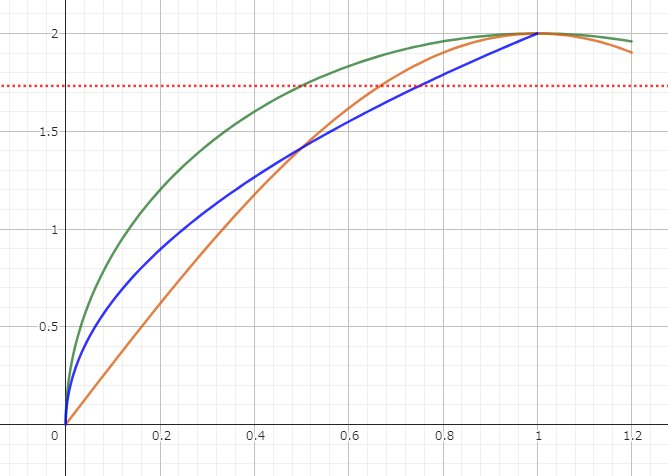
これらについて、縦軸を弦の長さとしてスケールを合わせ、1つの座標平面にまとめてみると、次のようになる。

（1）変数θ　 オレンジ y=2sin((π/2)ｘ)

（2）変数ｘ 緑 y＝2√(2ｘ-ｘ^2) 

（3）変数ｔ 紺 y＝2√ｘ

弦の長さが、√3よりも大きくなる（内接する正三角形の一辺より長くなる）ところは、それぞれ、

（1）オレンジ 0.66以上

（2）緑 0.5以上

（3）紺 0.75以上　になっていることが分かる。

すなわち、

（1）円周上に2点をとった場合、弦が√3より大きくなる確率は、1/3

（2）直径（半径）上に1点をとった場合、弦が√3より大きくなる確率は、1/2

（3）円の内部に1点をとった場合、弦が√3より大きくなる確率は、1/4　

となることが、弦の長さを調べた数式からも確かめられる。