リーグ戦の勝敗とゲーム差（7）

 (19) 4・3・2・2・2・2について
4勝チーム、3勝チーム、2勝チームの一つに注目して、整理すると、

AがBに負ける場合は、24通りあるが、

AがCまたはDまたはEまたはFに負ける場合は、それぞれ14通りずつになる。
合計80通りについて、入れ替えを行うと、6C4×2C1×80＝2400（通り）。

(20) 3・3・3・3・3・0について

(10)の場合と同様に、「3・3・3・3・3」は、5チームの対戦で「2・2・2・2・2」が起こる場合の数（24）に、全敗の6チーム目が加わったと考えて、24×6＝144（通り）。

(21) 3・3・3・3・2・1について
1勝チーム、2勝チーム、3勝チームの一つに注目して、整理すると、

FがEに勝つ場合は、24通りあり、

FがDまたはCまたはBまたはAに勝つ場合は、それぞれ14通りずつになる。
合計80通りで、入れ替え分を考えると、6C4×2C1×80＝2400（通り）。

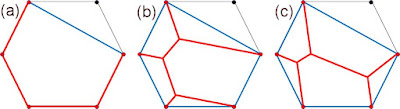
(22) 3・3・3・2・2・2について
2勝3敗の3チームに注目し、3チームにおける2つの○の配置を考えるのだが、これを予想するのは難しい。Fが勝つ2チームの組は、(D,E),(C,E),(C,D),(B,E),(B,D),(B,C),(A,E),(A,D),(A,C),(A,B)の10通りあるので、それぞれについて調べてみると、

(D,E)の場合で、24通り。

(C,E),(C,D),(B,E),(B,D),(A,E),(A,D)の場合で、それぞれ14通り。

(B,C),(A,C),(A,B)の場合で、それぞれ8通りがあることが分かる。
これらの合計は、24＋14×6＋8×3＝132（通り）で、入れ替えが、6C3＝20（通り）なので、全体では、20×132＝2640（通り）になる。

6チームによる試合のこれまでの結果をまとめてみると、次のようになる。
(1)　5・4・3・2・1・0　　ゲーム差［―,1,2,3,4,5］　  720（0.022）
(2)　5・4・3・1・1・1　　ゲーム差［―,1,2,4,4,4］　  240（0.007）
(3)　5・4・2・2・2・0　　ゲーム差［―,1,3,3,3,5］　  240（0.007）
(4)　5・4・2・2・1・1　　ゲーム差［―,1,3,3,4,4］　  720（0.022）
(5)　5・3・3・3・1・0　　ゲーム差［―,2,2,2,4,5］　  240（0.007）
(6)　5・3・3・2・2・0　　ゲーム差［―,2,2,3,3,5］　  720（0.022）
(7)　5・3・3・2・1・1　　ゲーム差［―,2,2,3,4,4］　1440（0.044）
(8)　5・3・2・2・2・1　　ゲーム差［―,2,2,3,3,4］　1680（0.051）
(9)　5・2・2・2・2・2　　ゲーム差［―,3,3,3,3,3］　  144（0.004）
(10) 4・4・4・2・1・0　　ゲーム差［―,0,0,2,3,4］　  240（0.007）
(11) 4・4・4・1・1・1　　ゲーム差［―,0,0,3,3,3］　    80（0.002）
(12) 4・4・3・3・1・0　　ゲーム差［―,0,1,1,3,4］　  720（0.022）
(13) 4・4・3・2・2・0　　ゲーム差［―,0,1,2,2,4］　1440（0.044）
(14) 4・4・3・2・1・1　　ゲーム差［―,0,1,2,3,3］　2880（0.088）
(15) 4・4・2・2・2・1　　ゲーム差［―,0,2,2,2,3］　1680（0.051）
(16) 4・3・3・3・2・0　　ゲーム差［―,1,1,1,2,4］　1680（0.051）
(17) 4・3・3・3・1・1　　ゲーム差［―,1,1,1,3,3］　1680（0.051）
(18) 4・3・3・2・2・1　　ゲーム差［―,1,1,2,2,3］　8640（0.264）
(19) 4・3・2・2・2・2　　ゲーム差［―,1,2,2,2,2］　2400（0.073）
(20) 3・3・3・3・3・0　　ゲーム差［―,0,0,0,0,3］　  144（0.004）
(21) 3・3・3・3・2・1　　ゲーム差［―,0,0,0,1,2］　2400（0.073）
(22) 3・3・3・2・2・2　　ゲーム差［―,0,0,1,1,1］　2640（0.081）
　　　　　　　　　　　　　　　　　　　　合計　　32768（ 1.00 ）

32,768通りの勝敗パターンがすべて同様に確からしい（起こりやすさが同じ）としたとき、(1)～(22)の事象の確率は、右端の（ ）内の数値になる。
これを見ると、ゲーム差が［―,1,2,3,4,5］（(1)の場合）になるのは、約2.2%ということで、めったに見られないというのは確かだが、22種類もの事象に散らばることによって、それぞれの確率が小さくなったからともいえる。

確率2.2％（720通り）の事象は4つあり、全22個のうち、上から12番目、下から8番目に位置するので、相対的に「とても低い」とはいいがたい。

むしろ、パターン（11）の「3チームが4勝1敗、3チームが1勝4敗」という、ゲーム差［―,0,0,3,3,3］が現実に起こったら、これはかなり珍しい（約0.2%）といってよいだろう。

しかし、勝ち数・負け数・勝率・ゲーム差が規則的に階段状に並ぶ、3/30の順位表はやはり美しく、特別な現象として話題になってもおかしくない。

ちなみに、3/31時点での結果もなかなか美しいのだが、1戦ずつの総当たりではない（6チームで合計18試合を行った）ので、勝ち数・負け数・勝率・ゲーム差を、均等に階段状に並べることはそもそもできない。

リーグ戦の勝敗とゲーム差（6）

(10) 4・4・4・2・1・0について

全敗のFチームが現れて、5チームに1勝ずつ与えたとすると、A～Eの5チームの勝ち数「4・4・4・2・1」は、太枠内での「3・3・3・1・0」に相当する。
5チームの際の「3・3・3・1・0」は40通りあったので、全敗の可能性が6チームともにあることから6倍することで、40×6＝240（通り）。

(11) 4・4・4・1・1・1について
3チームが4勝1敗、3チームが1勝4敗になるということは、上位3チームはいずれも下位3チームのすべてに勝利していなければならない。

つまり、上位3チームが互いに「1勝1敗」の関係、下位3チームが互いに「1勝1敗」の関係になる場合しかあり得ない。
太枠はそれぞれ2通りずつなので、この上位「ABC」と下位「DEF」の並びで、4通りある。
そして、上位3チームを選ぶのが、6C3＝20通りあるので、全部で、4×20＝80（通り）ある。

(12) 4・4・3・3・1・0について
(10)の場合と同様に、「4・4・3・3・1」は、5チームの対戦の「3・3・2・2・0」の場合の数に、全敗の6チーム目が加わったと考えて、120×6＝720（通り）。

(13) 4・4・3・2・2・0について
(10)の場合と同様に、「4・4・3・2・2」は、5チームの対戦の「3・3・2・1・1」の場合の数に、全敗の6チーム目が加わったと考えて、240×6＝1440（通り）。

(14) 4・4・3・2・1・1について
1勝4敗の2チームに注目して表を埋めていく。1勝4敗のチームをE,Fとし、FがEに勝った場合は、次のような8通りに限定される。

下から順に、黒色の○×を配置していくと、赤色の○×の部分は必然的に決定される。太枠はその内部で1勝1敗の状態を表し、2通りある。
同じく1勝4敗のチームをE,Fとし、FがEに負けた場合を考えると、次の8通りになる。

FがEに負け、AまたはBまたはCに勝ったとき、その他の勝敗はかなり限定的になることがわかる。
このように、4勝がA,B、3勝がC、2勝がD、1勝がE,Fとしたとき、16通りが存在する。
よって、入れ替えを考えると、6C2×4C2×2C1×16＝2880（通り）となる。

(15) 4・4・2・2・2・1について
まず、1勝4敗のチームがどこに勝ったかで場合分けし、次に4勝1敗の2チームが負けた相手を選んでいく。
1勝チームをFとし、4勝チームをA,Bとするとき、FがEまたはDまたはCに勝った場合は、それぞれ8通りずつのパターンが存在する。
FがEに勝ったとき

FがDに勝ったとき

FがCに勝ったとき

このように同じ傾向が見られるのだが、FがAまたはBに勝った場合は、ほぼ全体の勝敗が必然的に決まることになり、様子が大きく異なる。

具体的には、それぞれ2通りずつしかない。
以上のことから、全体として、28通りのパターンが存在する。また、4勝が2チーム、2勝が3チームあることから、チームの入れ替えを考えると、6C2×4C3×28＝1680（通り）がある。

(16) 4・3・3・3・2・0について
(10)の場合と同様に、「4・3・3・3・2」は、5チームの対戦の「3・2・2・2・1」の場合の数に、全敗の6チーム目が加わったと考えて、280×6＝1680（通り）。

(17) 4・3・3・3・1・1について
1勝の2チームと4勝の1チームの○×の組合せを考えると、

FがEに勝ち、EがBまたはCまたはDに勝つのがそれぞれ4通りあるが、EがAに勝つのは2通り。

FがBまたはCまたはDに勝つのがそれぞれ4通りあるが、FがAに勝つのは2通り。
これらを合わせて、28通りのパターンが見られる。
チームの入れ替えが、6C3×3C2＝60 なので、全体では、60×28＝1680（通り）。

(18) 4・3・3・2・2・1について
1勝チーム、4勝チーム、3勝チームの1つに注目して、整理してみた。

FがDまたはEに勝つ場合が、それぞれ14通りずつ。

FがBまたはCに勝つ場合が、それぞれ8通りずつ。

FがAに勝つ場合が、4通りある。
これらを合計すると48通りあり、チームの入れ替えにより、全体として、6C2×4C2×2C1×48＝8640（通り）ということになる。

リーグ戦の勝敗とゲーム差（5）

［5］6チームの場合

ついにプロ野球の結果を分析するチーム数までやってきた。
6チームが総当たりで1回ずつ試合を行うと、合計15試合になる。
わずか15試合ではあるが、どのチームがどこのチームに勝つかといったパターンは、全部で、2^15＝32,768通りもある。

そして、異なる勝率・ゲーム差の現れる勝敗パターンとしては、次のようなものが考えられる。
(1)　5・4・3・2・1・0
(2)　5・4・3・1・1・1
(3)　5・4・2・2・2・0
(4)　5・4・2・2・1・1
(5)　5・3・3・3・1・0
(6)　5・3・3・2・2・0
(7)　5・3・3・2・1・1
(8)　5・3・2・2・2・1
(9)　5・2・2・2・2・2
(10) 4・4・4・2・1・0
(11) 4・4・4・1・1・1
(12) 4・4・3・3・1・0
(13) 4・4・3・2・2・0
(14) 4・4・3・2・1・1
(15) 4・4・2・2・2・1
(16) 4・3・3・3・2・0
(17) 4・3・3・3・1・1
(18) 4・3・3・2・2・1
(19) 4・3・2・2・2・2
(20) 3・3・3・3・3・0
(21) 3・3・3・3・2・1
(22) 3・3・3・2・2・2　　以上、22通り

これら22通りの形で表される事象について、それぞれ何通りの場合があり、どれくらい起こりやすいか（起こりにくいか）を調べようと思う。

(1)　5・4・3・2・1・0について

５チームでの「4・3・2・1・0」の場合（太枠内で起こる結果、この場合120通り）をそのままに、新たなFチームが現れて5連勝したと考える。５勝するチームの可能性は、A～Fの６チームともにあるので、120×6＝720（通り）となる。

(2)　5・4・3・1・1・1について
上と同様に、5チームでの「4・3・1・1・1」が40通りあったことから、新たに5勝するチームが6通り考えられて、40×6＝240（通り）。

(3)　5・4・2・2・2・0について
同様に、5チームでの「4・2・2・2・0」が40通りあったので、40×6＝240（通り）。

(4)　5・4・2・2・1・1について
同様に、5チームでの「4・2・2・1・1」が120通りあったので、120×6＝720（通り）。

(5)　5・3・3・3・1・0について
同様に、5チームでの「3・3・3・1・0」が40通りあったので、40×6＝240（通り）。

(6)　5・3・3・2・2・0について
同様に、5チームでの「3・3・2・2・0」が120通りあったので、120×6＝720（通り）。

(7)　5・3・3・2・1・1について
同様に、5チームでの「3・3・2・1・1」が240通りあったので、240×6＝1440（通り）。

(8)　5・3・2・2・2・1について
同様に、5チームでの「3・2・2・2・1」が280通りあったので、280×6＝1680（通り）。

(9)　5・2・2・2・2・2について
同様に、5チームでの「2・2・2・2・2」が24通りあったので、24×6＝144（通り）。

というわけで、「5」のついた、ここまでの事象の場合の数については、シンプルに求めることができた。

リーグ戦の勝敗とゲーム差（4）

(5) 3・3・3・1・0
(6) 3・3・2・2・0　の場合について、
「0」が1つあるとき、全敗のEチームが登場し、4チームで対戦したA,B,C,Dに対して1勝ずつ与えたと考える。すると、「3・3・3・1・0」について、これを引き算したもの（太枠の色のついた部分）は前回の「2・2・2・0」と同じ、「3・3・2・2・0」は、前回の「2・2・1・1」と同じと考えられる。つまり、

(5) 3・3・3・1・0について
前回の「2・2・2・0」が8通りだったので、全敗になるチームの可能性を5通りと考えて、8×5＝40（通り）。

(6) 3・3・2・2・0について
前回の「2・2・1・1」が24通りだったので、24×5＝120（通り）。

(7) 3・3・2・1・1について
上位2チームが「3・3」となる場合を具体的に考えてみる。

水色のマスを埋めることで、必然的に決まってくるマス（赤色の○×）が多く存在し、上のような8通りしか存在しないことが分かる。
ただし、上記のA,B,C,D,Eの順番（3・3・2・1・1の割り振り）は一例なので、これを入れ替えたすべての場合を求める必要がある。

つまり、「3勝」が2チーム、「1勝」が2チームあるので、入れ替えによって、5C2×3C2＝30 倍 の場合が考えられることから、8×30＝240（通り）になる。

(8) 3・2・2・2・1について
「3」と「1」に注目して表を埋めていくと、

Aを3勝チームとして×の箇所を1つ選び、Eを1勝チームとして○の箇所を1つ選ぶと、ほぼ必然的に他が決定する。太枠の3×3のマス目は3チームが1勝ずつすればよいところで、2通りずつあることを示す。
上のような14通りがあることが分かったが、今回は「2」が3チームあるので、入れ替えパターンとしては、5C3×2C1＝20 倍 を考えねばならない。
したがって、14×20＝280（通り）になる。

(9) 2・2・2・2・2について
すべてのチームが2勝するということで、とりあえず、2チームの2勝の箇所を埋めていく。

上の表で、AとBの2勝の箇所を埋めると、残り3チームの○×の配置がすべて確定することが分かった。太枠のところは2通りの配置ができるところなので、全部で24通りということになる。
全チームが同じ2勝2敗であることから、入れ替えても、上記24通りのいずれかになるので、これがすべてである。

以上、(1)～(9)を整理すると、
(1) 4・3・2・1・0　　120通り
(2) 4・3・1・1・1　　 40通り
(3) 4・2・2・2・0　　 40通り
(4) 4・2・2・1・1　　120通り
(5) 3・3・3・1・0　　 40通り
(6) 3・3・2・2・0　　120通り
(7) 3・3・2・1・1　　240通り
(8) 3・2・2・2・1　　280通り
(9) 2・2・2・2・2　　 24通り

これらを合計すると、120＋40＋40＋120＋40＋120＋240＋280＋24＝1024　となり、漏れなく場合の数が数えられているようだ。

5チームが総当たり戦を行った場合、そのゲーム差が「1，2，3，4」になるのは(1)の場合だけなので、このような結果が現れるのは、120/1024（0.117）の確率となる。
ちなみに、5チームが同率で並ぶような結果（9）が出るのは、24/1024（0.023）で、滅多に見られない現象と考えてよい。

リーグ戦の勝敗とゲーム差（3）

［4］5チームの場合

A,B,C,D,Eの5チームが総当たり戦を行うと、全部で10試合を行うことになる。

このとき、右上の10マスに○か×を埋めるパターンは、2^10＝1024 あるので、勝敗のパターンは全部で1024通りあることになる。
勝敗パターンを表に埋め込んでいくと、×に置き換えたマスの配置が規則正しく変化していく。これは、2進法の記号とみなすこともできそうだ。

5チームが、それぞれ他の4チームと試合を行うとき、ゲーム差が異なる勝敗パターンとしては、次のような9通りが考えられる。

(1) 4・3・2・1・0（4勝・3勝・2勝・1勝・0勝の5チームができるという意味）
(2) 4・3・1・1・1
(3) 4・2・2・2・0
(4) 4・2・2・1・1
(5) 3・3・3・1・0
(6) 3・3・2・2・0
(7) 3・3・2・1・1
(8) 3・2・2・2・1
(9) 2・2・2・2・2

これらがそれぞれ何通り存在するかを調べるのは、けっこうたいへんそうだが、「あきらめずに考え」ていこう。

(1) 4・3・2・1・0
(2) 4・3・1・1・1
(3) 4・2・2・2・0
(4) 4・2・2・1・1　の4つの場合について、
最初の「4」を除くとそれぞれ、

(1) 3・2・1・0、(2) 3・1・1・1、(3) 2・2・2・0、(4) 2・2・1・1

になる。これは、「［３］４チームの場合」ですでに調査済みのものである。つまり、下図のように、４チームの勝敗パターンの上に全勝チームを１つ加えたものとして扱うことができる。

全勝チームは、５チームのいずれかなので、前回の4チームの結果を５倍すればよい。したがって、
(1) 4・3・2・1・0について
前回の「3・2・1・0」が24通りだったので、24×5＝120（通り）

(2) 4・3・1・1・1について
前回の「3・1・1・1」が8通りだったので、8×5＝40（通り）

(3) 4・2・2・2・0について
前回の「2・2・2・0」が8通りだったので、8×5＝40（通り）

(4) 4・2・2・1・1　の4つの場合について、
前回の「2・2・1・1」が24通りだったので、24×5＝120（通り）

といった具合になる。

リーグ戦の勝敗とゲーム差（2）

［3］4チームの場合

A,B,C,Dの4チームが、総当たり戦を行うと、合計6試合を行うことになる。
たとえば、Aが3勝、Bが2勝、Cが1勝したときの対戦表はこんな感じだ。（「×」は省略）

対戦結果の可能性は、右上の6つのマスに○か×をつける場合の数を数えることになるので、2^6＝64 通りが考えられる。

また、異なるゲーム差が生じる勝敗パターンとしては、
(1) 3勝・2勝・1勝・0勝
(2) 3勝・1勝・1勝・1勝
(3) 2勝・2勝・1勝・1勝
(4) 2勝・2勝・2勝・0勝　の4通りが考えられ、かつ、これ以外にない。

64通りを並列に並べて調べる方法もあるが、(1)～(4)がそれぞれ何通りあるかを考える方が早そうだ。

(1) 3勝・2勝・1勝・0勝について
3勝するチームとしてA,B,C,Dの4通り、2勝するチームはその3連勝チームを除く3通り、1勝するチームは上位2チームを除いた2通り、0勝チームは残された1通り。

よって、4×3×2＝24（通り）。

(2) 3勝・1勝・1勝・1勝について
3勝するチームはA,B,C,Dの4通り、残る3チームが1勝ずつ分けるのは、［２］の(2)で扱った「 1勝・1勝・1勝」になるパターンなので、2通り。

よって、4×2＝8（通り）。

(3) 2勝・2勝・1勝・1勝について
2勝するチームが2つあるパターン（たとえば、A,Bが2勝する）を考えると、

という4通りになる。水色のマスを埋めたとき、「2・2・1・1」になるためには、残りのマスの○×は必然的に決定される。

（黒色の○×はマスを選んで入れたもので、赤色の○×はそこにしか入らなくなったものを示す。）
4チームのうち、上位2チームを選ぶ組合せは、4C2＝6通りなので、全体としては、6×4＝24（通り）となる。

(4) 2勝・2勝・2勝・0勝について
0勝のチームになる可能性はA,B,C,Dの4通りあるが、この場合、残りの3チームは互いに「 1勝・1勝・1勝」になること（2通りある）を意味する。

よって、4×2＝8（通り）。

(1)～(4)の場合の数を合計すると、24＋8＋24＋8＝64 となり、最初に求めた「2^6=64」に一致する。

これらの勝率とゲーム差について見てみると、
(1)の場合、勝率は「1.0、0.67、0.33、0.0」、ゲーム差は「―、1.0、2.0、3.0」
(2)の場合、勝率は「1.0、0.33、0.33、0.33」、ゲーム差は「―、2.0、2.0、2.0」
(3)の場合、勝率は「0.67、0.67、0.33、0.33」、ゲーム差は「―、0.0、1.0、1.0」
(4)の場合、勝率は「0.67、0.67、0.67、0.0」、ゲーム差は「―、0.0、0.0、2.0」

のようになる。
したがって、総当たり戦を終えて、ゲーム差が「1.0、2.0、3.0」になるのは、24/64（0.375）の確率になる。

ちなみに、すべての場合を列挙してみるとこうなる。

リーグ戦の勝敗とゲーム差（1）

いよいよ明日からプロ野球の日本シリーズが始まる。
2022年のセ・パ両リーグの最終勝率とゲーム差は次の通りであった。

実は、今シーズンが始まってまもなくの3月30日、セリーグの勝敗に興味深い結果が見られた。

ゲーム差が「1.0、2.0、3.0、4.0、5.0」と、規則正しく並ぶという現象が見られたのだ。珍しそうなので、この新聞記事を切り取っておいたのだが、果たしてこの現象はどれくらい珍しいのだろうか、というのが今回のテーマ。

ここでは、次のような条件の下で勝敗パターンを調べることとする。
・参加チームが1戦ずつの総当たり戦（リーグ戦）を行ったら終了。
・一試合ごとに勝敗が決まる（引き分けはない）。
・どのチームも同じ程度に強い（勝ち負けは、50/50）。

いきなり6チームの場合を考えるのは難しいので、少ないチーム数から調べてみよう。

［１］2チームの場合
AチームとBチームが、1試合を行った場合、
① Aが1勝、Bが1敗
② Aが1敗、Bが1勝
の２通りのいずれかであり、どちらも同程度に起こりうる。このとき、ゲーム差は必ず「1.0」になる。

［２］3チームの場合
Aチーム、Bチーム、Cチームが、異なる相手と合計3試合を行った場合、
① Aが2勝、Bが1勝、ｃが0勝
② Aが2勝、Bが0勝、ｃが1勝
③ Aが1勝、Bが2勝、ｃが0勝
④ Aが1勝、Bが0勝、ｃが2勝
⑤ Aが0勝、Bが2勝、ｃが1勝
⑥ Aが0勝、Bが1勝、ｃが2勝
⑦ Aが1勝、Bが1勝、ｃが1勝
のいずれかになるが、「⑦ Aが1勝、Bが1勝、ｃが1勝」には、2通りが考えられる。
上の状況を表にして書き直すと、

このように、８通りが見つけられる。
3チームの勝敗パターンが8通りになることについて、次のように説明することができる。

右上の黄色いマスの○×によって、左下のマスの○×は自動的に決まる。つまり、場合の数は、黄色の３つのマスに○まはた×を入れる方法が何通りあるかを数えればよい。
つまり、この場合、2^3＝8（通り）になるということだ。

次のようにも説明できる。
3チームで総当たり戦を行った場合の結果は、
(1) 2勝・1勝・0勝
(2) 1勝・1勝・1勝　の2通りある（2通りしかない）。
(1)については、A,B,Cの入れ替えが、3C1×2C1＝3×2＝6通り
(2)については、A＞B＞C（⑦）、A＜B＜C（⑧）のような関係で、2通り あることから、
これらを合わせて、8通りになる。

さて、このとき、勝率とゲーム差は次のようになる。
(1) の場合（①～⑥の場合）、勝率は「1.0、0.5、0.0」、ゲーム差は「―、1.0、2.0」、
(2) の場合（⑦～⑧の場合）、勝率は「0.5、0.5、0.5」、ゲーム差は「―、0.0、0.0」　となる。
したがって、3試合を終えて、ゲーム差が「―、1.0、2.0」（自然数列）になるのは、6/8（0.75）の確率といえる。

シャボン膜の形と長さ（13）

これまでのシャボン膜の実験をまとめておこう。

① 三角形の場合

　(a) 二等辺三角形　　(b) 直角三角形　　(c) 正三角形

(a)　3辺の長さ：2＋√3 シャボン膜の長さ：2 膜／辺：0.54
(b)　3辺の長さ：3＋√3 シャボン膜の長さ：√7 膜／辺：0.56
(c)　3辺の長さ：3√3 シャボン膜の長さ：3 膜／辺：0.58

② 四角形の場合

　(a) 等脚台形　　(b) たこ形　　(c) 長方形

(a)　4辺の長さ：5　 シャボン膜の長さ：3            膜／辺：0.60
(b)　4辺の長さ：2＋2√3 シャボン膜の長さ：√13        膜／辺：0.66
(c)　4辺の長さ：2＋2√3     シャボン膜の長さ：2√3        膜／辺：0.63

③ 五角形の場合

　(a) 0°対辺　　(b) 30°対辺　　(c) 60°対辺

(a)　5辺の長さ：4＋√3        シャボン膜の長さ：4            膜／辺：0.70
(b)　5辺の長さ：4＋√3        シャボン膜の長さ：√21        膜／辺：0.80
(c)　5辺の長さ：4＋√3        シャボン膜の長さ：√19        膜／辺：0.76

④ 六角形の場合

　(a) ハ型　　(b) ニ型　　(c) ロ型

(a)　6辺の長さ：6        シャボン膜の長さ：5        膜／辺：0.83
(b)　6辺の長さ：6        シャボン膜の長さ：2√7    膜／辺：0.88
(c)　6辺の長さ：6        シャボン膜の長さ：3√3    膜／辺：0.87

今回の実験の条件下では、

・「膜／辺」の比率 r は、0.5＜ r ＜ 1 であること

・頂点の数が増えるにしたがって、「膜／辺」の比率も大きくなること

などが読み取れる。

調べていくとさらに調べたいことが次々に現れてくるのが「探究」の面白さ。

とはいえ、今回のテーマはこの辺で「まく」を閉じたい。

シャボン膜の形と長さ（12）

④－(c) 六角形「ロ型」の場合

シャボン膜は、120°で交わる三叉路が4つつながった折れ線になる。（写真は2004年のときのもの）

枝分かれが対称的で、シャボン膜全体の長さは求めやすい。

これを1本の線分にまとめる方法は次の通り。

3方向に小さな正三角形（△AFG、△BCH、△DEI）を描き、2つの正三角形を含む大きな正三角形HIJを描く。上の図の2点G、Jを結ぶ線分が今回のシャボン膜を1本にまとめたものになる。

線分GJのうち、LJは、LH＋LIに置き換えられ、LGは、LK＋KA＋KFに置き換えられる。
さらに、線分LHは、LM＋MB＋MCに、線分LIは、LN＋ND＋NEに置き換えることができて、シャボン膜全体の長さは、線分GJの長さに等しいことがわかる。
よって、膜の全長は、3√3 である。

今回の図は、正三角形に対するシャボン膜の構造が、3つ連なったものともいえる。
BM＋CM＋LM＝LH より、ひとつ分の長さは、√3である。
したがって、全体の長さは、3√3 であることが確かめられる。

シャボン膜の形と長さ（11）

④－(b) 六角形「ニ型」の場合

シャボン膜は、120°で交わる三叉路が4つつながった折れ線になる。（写真は2004年のときのもの）

この網目のような折れ線を一本の直線で表す作図について、これまでの手順に倣ってやってみる。
「ニ型」ということで、辺AFと辺CDに注目し、そこに正三角形AFGを描き、その頂点と残した1点Bを結ぶ線分で新たな正三角形BGIを描く。
反対側も同様に、正三角形EHJをつくって、その頂点同士を結んだ線分IJが、今回のシャボン膜の構造を表すものとなるだろう。

IKの長さは、KBとKGの長さの和に等しく、LJの長さは、LEとLHの長さの和に等しい。
すなわち、一旦は、平行四辺形GBHEの4頂点を結ぶシャボン膜を形成させてから、次の段階を考える。

上図より、KGの長さは、KMとMAとMFの和の形に表せ、LHは、LN＋NC＋NDで表せることが分かる。
すなわち、膜をつくる9本の線分の和は、もとの図の線分IJの長さに一致する。
そして、その長さは、IP＝2√3、PJ＝4 より、IJ＝2√7 になる。

今回のシャボン膜の形状は、平行四辺形ABOFと平行四辺形OCDEについてできるシャボン膜が2つ手をつないでいるようにも見える。
平行四辺形ABOFにおけるシャボン膜の長さは、GCの長さに等しいので、GC^2＝((3√3)/2)^2＋(1/2)^2＝7 から求めても、赤いシャボン膜全体の長さは、やはり 2√7 になる。