シャボン膜の形と長さ（13）

これまでのシャボン膜の実験をまとめておこう。

① 三角形の場合

　(a) 二等辺三角形　　(b) 直角三角形　　(c) 正三角形

(a)　3辺の長さ：2＋√3 シャボン膜の長さ：2 膜／辺：0.54
(b)　3辺の長さ：3＋√3 シャボン膜の長さ：√7 膜／辺：0.56
(c)　3辺の長さ：3√3 シャボン膜の長さ：3 膜／辺：0.58

② 四角形の場合

　(a) 等脚台形　　(b) たこ形　　(c) 長方形

(a)　4辺の長さ：5　 シャボン膜の長さ：3            膜／辺：0.60
(b)　4辺の長さ：2＋2√3 シャボン膜の長さ：√13        膜／辺：0.66
(c)　4辺の長さ：2＋2√3     シャボン膜の長さ：2√3        膜／辺：0.63

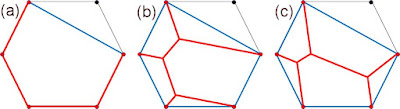
③ 五角形の場合

　(a) 0°対辺　　(b) 30°対辺　　(c) 60°対辺

(a)　5辺の長さ：4＋√3        シャボン膜の長さ：4            膜／辺：0.70
(b)　5辺の長さ：4＋√3        シャボン膜の長さ：√21        膜／辺：0.80
(c)　5辺の長さ：4＋√3        シャボン膜の長さ：√19        膜／辺：0.76

④ 六角形の場合

　(a) ハ型　　(b) ニ型　　(c) ロ型

(a)　6辺の長さ：6        シャボン膜の長さ：5        膜／辺：0.83
(b)　6辺の長さ：6        シャボン膜の長さ：2√7    膜／辺：0.88
(c)　6辺の長さ：6        シャボン膜の長さ：3√3    膜／辺：0.87

今回の実験の条件下では、

・「膜／辺」の比率 r は、0.5＜ r ＜ 1 であること

・頂点の数が増えるにしたがって、「膜／辺」の比率も大きくなること

などが読み取れる。

調べていくとさらに調べたいことが次々に現れてくるのが「探究」の面白さ。

とはいえ、今回のテーマはこの辺で「まく」を閉じたい。