ランダムに引いた弦の長さ（6）

「円の中にランダムに引いた弦の長さ」について、また違った方法を考える。

（3）円の内部に適当な点をとり、その点が中点となるような弦の長さはどれくらいになるか。

⑤ 方法5

下図のように、中心が原点にある単位円の内部に適当な点Aをとり、OAに垂直な直線を引くとき、点Aを中点とする弦BCが引ける。円の内部にランダムな点をとった場合に、この弦BCの長さの平均を求めたい。

これまでとは異なり、点Aは2次元表記が必要になる。

点Aは、直交座標で、(x,y) （ただし、0≦ｘ≦1、0≦ｙ≦1、0≦x^2＋y^2≦1）と表す方法もあるし、

極座標で、(r,θ) （ただし、0≦ｒ≦1、0≦θ≦2π）と表す方法もある。ここでは極座標を用いて考える。

A(r,θ)を定めるとき、弦BCの長さは、2√(1－r^2) と表せる。θ は弦の長さには影響しない。

しかし、同じθ座標をもつOD上の点であっても、座標ｒが大きくなる（外周に近づく）と、その一周（点線）の長さが長くなることから、選ばれやすさも大きくなると思われる。

点Aと同じ半径ｒをもつ点の集まりは、2πrの長さの円周上の点であり、点A'と同じ半径r'をもつ点の集まりは、2πr'の長さの円周上の点であることから、点Aに対する点A'の選ばれやすさは、r'：r といえるだろう。

点Aよりも内側の点が選ばれる確率（πr^2/π）に対して、点A'より内側の点が選ばれる可能性（πr'^2/π）は、r'^2：r^2 、すなわち、半径の比（r'/r）の2乗に比例するという言い方もできる。

ランダムに引いた弦の長さ（5）

引き続き、③と④の「確率測度の違い」について考える。

③の場合、CD＝2sinθと表すことができて、θが 0→π/2 で変化するときのCDの長さの平均を求めた。

いま、第1象限と第2象限におけるBCの長さの平均を求めるとしたとき、

f(θ)＝sinθで表される曲線とθ軸に挟まれた部分の面積をπで割れば、この山の高さ（BCの長さ）の平均が求められる。

上図のサインカーブの面積は 2 なので、ここから導かれるBCの長さの平均は、2÷π＝2/π≒0.637　となる。（2倍すると、1.27）

円周上の点に着目してその変化を追うということは、動径の「θ」が変数になっている。

一方、④の場合、AB間の距離をxと置き直したとき、CD＝2√(2x-x^2) と表すことができて、ｘが0→1で変化するときの長さの平均を求めた。

上記と同様に、第1象限と第2象限におけるBCの長さの平均を求めるとすると、

f(x)＝√(2x-x^2) で表される曲線（半円）とｘ軸に挟まれた部分の面積を2で割れば、BCの平均が求められる。

半径が1の半円の面積は、π/2 なので、導かれるBCの長さの平均は、π/2÷2＝π/4≒0.785　となる。（2倍すると、1.57）

半径（直径）上の点に着目してその変化を追うのは、線分上の位置「ｘ」が変数になっているということだ。

③と④のグラフの曲線は、縦軸においては、0→1 の同様の変化を表しているわけだが、横軸の動きの違いによって、サインカーブと半円のカーブに描き分けられているともいえる。

したがって、③のグラフの、縦軸はsinθの値（そのまま）で、横軸をθでなく、1-cosθ をとるようにプロットするならば、それは、④の半円のカーブを描くことになる。

ランダムに引いた弦の長さ（4）

求めた弦CDの平均値は、③で「4/π」、④で「π/2」となり、これは確率測度の違いによるものということであった。

だが、③と④のどこに違いがあるかについて説明するのは難しい。これについてもう少し考えてみよう。

下図のように、まず円周を等間隔に区切って点を打つ。そしてこの点を通りｘ軸に垂直な直線を引いてみると、これらの平行線は等間隔でなく、点Aに近いところで、平行線は密になっている。

円周上で点を動かすことによる弦の数え方と、半径上の点を動かしてつくった弦の数え方の違いを、この図は表しているといえるだろう。この疎密というのが、測度の違いを表しているのではないか。

①②③の方法は、少し見方は異なっているが、いずれも動径の動きを角度で表して円周上の点を均等に押さえていた。

たとえば、①の方法では、動径OBの端点Bと定点Aを結んで、弦ABの長さを考えた。

いま、円周上に15°刻みで24個の点を打ち、点Aと上半円上の点を結ぶ12本の弦の長さを計算すると、

2sin7.5°, 2sin15°, 2sin22.5°, 2sin30°, 2sin37.5°, 2sin45°, 2sin52.5°, 2sin60°, 2sin67.5°, 2sin75°, 2sin82.5°, 2sin90° となる。これらの近似値を求めると、0.26 , 0.52 , 0.77 , 1.00 , 1.22, 1.41 , 1.59 , 1.73 , 1.85 , 1.93 , 1.98 , 2.00 となって、

これら12本の弦の長さの平均は、1.35 となる。

一方、④の方法は、半径（または直径）上の点の位置に注目し、その線分上の点を均等に押さえていた。

すなわち、下図のように、半径OAに垂直な直線を一定間隔で平行移動させて弦CDの長さを考えた。

上の場合と同じように、半径を6等分する間隔で引いた平行線によってできた12本の弦の長さを計算してみると、

2√(1-(5/6)^2) , 2√(1-(4/6)^2) ,2√(1-(3/6)^2) , 2√(1-(2/6)^2) , 2√(1-(1/6)^2) , 2√(1-(0/6)^2) , 2√(1-(-1/6)^2) , 2√(1-(-2/6)^2) , 2√(1-(-3/6)^2) , 2√(1-(-4/6)^2) , 2√(1-(-5/6)^2) , 2√(1-(-6/6)^2) となる。これより近似値は、1.11 , 1.49 , 1.73 . 1.89 , 1.97 , 2.00 , 1.97 ,  1.89 , 1.73 , 1.49 , 1.11 , 0.00　となって、

これら12本の弦の長さの平均は、1.53 となる。 

ざっくりと有限の本数で比較してみた場合、④の方法の方が平均値は大きくなりそうである。無数の線を引く場合には状況が違ってくるだろうから、たかだか12本程度の比較では十分とはいえないのだが。

ランダムに引いた弦の長さ（3）

引き続き、円の中にランダムに引いた弦の長さを調べる。

（2）半径（直径）上に適当な点をとるとき、その点を通り半径に垂直な弦の長さはどれくらいになるか

④ 方法4

下図のように、中心が原点にある単位円の半径OA上に適当な点Bをとり、Bを通りOAに垂直な弦CDの長さに注目する。

定点A(1,0)、動点B(x,0) とすると、点Cの座標は、(x,√(1ーx^2))と表せ、CD＝2√(1ーx^2)　となる。

点Bを、0≦x≦1 で動かすときのCDの長さの平均値（期待値）を求めるためには、

2√(1ーx^2) を 0→1 の範囲で積分すればよい。

つまり、上のグラフは、f(x)＝2√(1ーx^2)（0≦ｘ≦1）を示すが、x軸、y軸、f(x)で囲まれた面積は、

x＝sinθ とおいて置換積分して、2((cosθ)^2)･cosθ＝1＋cos(2θ)  を 0→π/2 で積分することになり、［θ＋(1/2)sin(2θ)］( 0→π/4)＝π/2　となる（半円の面積）。

これを (1ー0＝1) の範囲で割って、その平均値は、π/2　およそ、1.57　となる。

③と④を比べてみよう。

③では、∠COA＝θによって、弦CD＝2sinθ と定義し、0≦θ≦π/2 の範囲でその変化を扱い、

④では、点Bの座標をｘとして、弦CD＝2√(1ーx^2) と定義し、0≦ｘ≦1 の範囲でその変化を扱った。

どちらも、右半円の領域で、CDの長さを0から2まで変化させていることに変わりないのだが、

③では、平均値が、4/π（≒1.27）

④では、平均値が、π/2（≒1.57）　という違いが現れた。

これは、円周上の点の集合を1（全体）としたものと、半径上の点の集合を1（全体）としたものの違い（確率測度の違い）によると考えられる。よく似たアプローチで解いているが、測度が異なると結果（平均の長さ）も異なるのである。

ランダムに引いた弦の長さ（2）

 

（1）円周上にランダムに2点をとるとき、2点間の距離はどれくらいになるか、の続き

③ 方法3

始線OAと動径OBのなす角をθとしつつ、弦の端点として点Aを使わずに、OAに垂直な線分BCによって、弦を定める。

この場合、ランダムとった2点としてはこれまで通り、A,B なのだが、A,B によって必然的に定められた点Cを用いて、BC間の距離を測るといった方法をとっている。

OB＝1より、BC＝2sinθと表せるので、前回の「② 方法2」と同じように、BCの長さについて、θ を 0→π/2 の範囲で積分して、π/2で割る作業を行う。

その平均値は、2÷(π/2)＝4/π　およそ、1.27　となる。

②と③を比べてみると、

②において、接線と弦のなす角がθのとき、∠AOB'（＝2θ）の対辺AB'の長さを考えたが、これは、③における、∠BOC（＝2θ）の対辺、すなわちOAに垂直な線分BCの長さに相当することがわかる。

このように、円周上にランダムに2点をとるとした考え方だけでも、いくつかの方法があるのだが、基本的に、動径OBを回転運動させ、点Bの経路である半円周を「1」とした確率（期待値）を扱っているという点で共通である。

さらに、点Bに対して、y軸に垂直な弦をとるような設定もできる。この場合、BCはこれまでとは違って、AB'に一致しない。しかし、下図より、BC＝ 2cosθとなることから、θ を 0→π/2 で積分して、π/2で割れば、同じ結果が得られることがわかる。

ランダムに引いた弦の長さ（1）

いよいよ「ベルトランのパラドックス」に関わる「円にひいた弦」について考えていこう。

円の中にランダムに引いた弦の長さはどれくらいか、その弦の長さの平均値（期待値）を求めようというものである。

まず初めに「ランダムに引く弦」をどのように定義するか、を明らかにしておく必要がある。

いくつかの方法があるので、順に調べてみたい。

（1）円周上に適当な2点をとるとき、2点間の距離はどれくらいになるか。

① 方法1

下図のように、原点を中心とする半径1の円を描き、点A(1,0)を固定して、適当な点B(x,y)までの距離を測ることを考える。

点Bは上半円の円周上にあるものを考えれば十分であろう。

この場合、点Bの座標は、始線OAと動径OBのなす角θを用いて、(cosθ,sinθ) と表せるので、

AB＝√((1ーcosθ)^2＋(sinθ)^2)　

　 =√(1-2cosθ＋(cosθ)^2＋(sinθ)^2)

　 ＝√(2(1ーcosθ))＝√(4･(sin(θ/2))^2)＝2sin(θ/2)　と表せる。

点Bを、0≦θ≦πで動かすときのABの長さの平均値（期待値）を求めればよいので、

2sin(θ/2) を 0→π で積分して ［－4cos(θ/2)］( 0→π)＝4、これを (πー0) の範囲で割ればよいから、

その平均値は、4÷π＝4/π　およそ、1.27　となる。

② 方法2

①のときと同様に、原点を中心とする半径1の円を描き、点A(1,0)を固定して、適当な点B(x,y)までの距離を測る。

ただし、点Aにおける接線ATと弦ABのなす角θを0からπ/2まで変化させるときの点Bの移動を考えている。

この場合、中心Oから弦ABに下ろした垂線の足をHとすると、∠TAB＝∠AOH （ともに90°－∠OAB）であり、

OA＝1 なので、AH＝sinθ、すなわち、AB＝2sinθ　となる。

2sinθ を 0→π/2 で積分して、［－2cosθ)］( 0→π/2)＝2、これを (π/2ー0) の範囲で割ればよいから、

その平均値は、2÷(π/2)＝4/π　およそ、1.27　となる。

①と②を比べてみると、

接弦定理より ∠TAB＝∠ACB、円周角の定理より ∠AOB＝2∠ACB がいえる。

①の考え方を使うと、θ＝φ/2 より、点Bの座標は、(cos(2θ), sin(2θ)) と表せるので、AB＝2sinθ　が導ける。

つまり、点Aのまわりに線分ABを回転させる考え方と、点Oのまわりに線分OBを回転させる考え方は同じということがわかる。

円周上の3点がつくる弧の長さ

円周上の2点の場合は簡単だったので、次に、円周上にランダムに3点をとるとき、いずれかの2点を結ぶ弧のうち、一番短い弧の長さはどれくらいか、を考える。

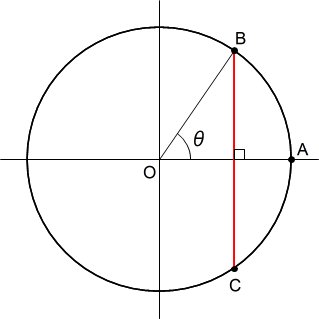
前回の2点の場合と同じく、単位円を用いて、弧の長さをその弧に対する中心角の大きさで扱うものとする。また、点Aを図のように固定した上で、点Bは上半円の円周上にある場合について考えれば十分であろう。

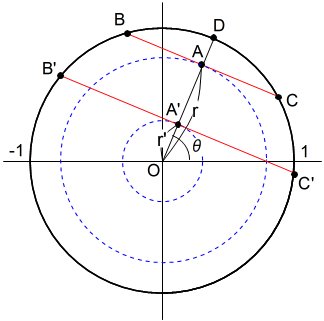
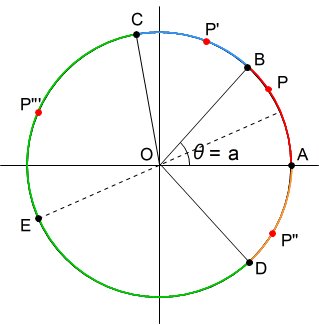
1点目のAを下図のように固定し、2点目のBに対する動径OBの回転角度をθとする。3点目のPの位置が下図の色分けされた弧にある場合をそれぞれ考えてみよう。

① 弧AB（赤色）上にあるとき、最短の弧の長さは、0から a/2 の値をとる。
② 弧BC（青色）上にあるとき、最短の弧の長さは、0から a の値をとる。
③ 弧AD（オレンジ）上にあるとき、最短の弧の長さは、0からa の値をとる。
④ 弧CED（緑色）上にあるとき、最短の弧の長さは、a（弧AB）となる。
なお、図中の点Eは、弧CD（緑色）の中点である。

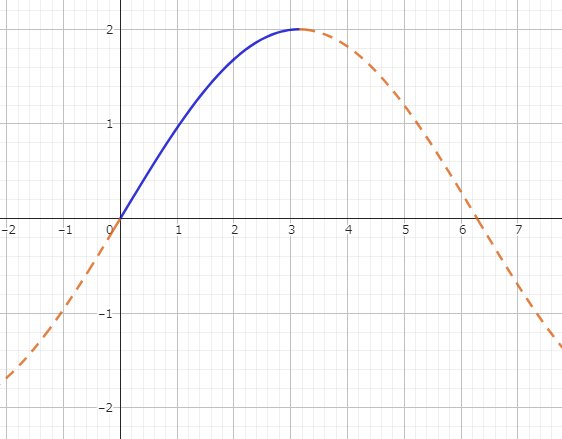
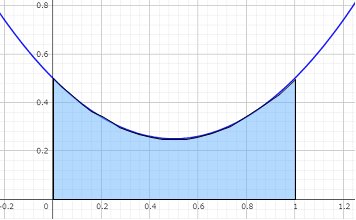
点Pの移動による最短の弧の長さの変化を図示すると次のようになる。
ただし、緑色の弧が存在するのは、動径OBの回転角度θが、0≦θ＜(2/3)π の範囲に限られる。

0≦θ≦(2/3)π における最短の弧の長さの平均（f(a)）は、青色の面積を全体の2πで割ることで求められる。
f(a)＝{(a/2)^2＋a^2＋2a(π-(3/2)a)}÷(2π)＝{2πa-(7/4)a^2}÷(2π)＝a-(7/(8π))a^2
a の値を 0から (2/3)π まで変化させたときの平均は、この f(a) を a で積分して、 (2/3)π で割ればよい。
a-(7/(8π))a^2 を (0→(2/3)π) で積分すると、
［(1/2)a^2-(7/(24π))a^3］(0→(2/3)π)＝(11/81)π^2
よって、{(11/81)π^2}÷(2/3)π＝(11/54)π　が求められた。

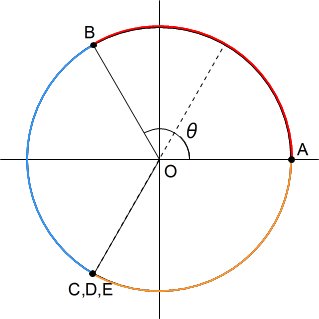
さて、θが(2/3)πに近づくにしたがって、4色に色分けた上図の緑色の弧は小さくなる。そして、θ＝(2/3)π のとき、C,D,Eは一致し、緑色の弧は消える。このとき、赤、青、オレンジの弧の長さはすべて  (2/3)π の長さになり、これが求める弧の長さの最大値となる。

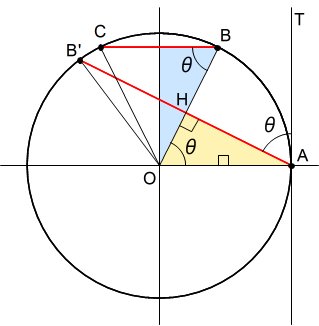
さらに(2/3)π＜θ≦π の場合を考えると、弧ABと同じ長さの弧BCと弧ADは重なり合うことになるので、弧BDCAを2等分し、弧BE（青色）と弧AE（オレンジ）に分けて、以下のように整理できる。

① 弧AB（赤色）上にあるとき、最短の弧の長さは、0から a/2 の値をとる。
② 弧BE（青色）上にあるとき、最短の弧の長さは、0から π-(a/2) の値をとる。
③ 弧AE（オレンジ）上にあるとき、最短の弧の長さは、0からπ-(a/2) の値をとる。

点Pの移動による最短の弧の長さの変化を図示すると次のようになる。

(2/3)π＜θ≦π における最短の弧の長さの平均（f(a)）は、青色の面積を全体の2πで割ることで求められる。
f(a)＝{(a/2)^2＋(π-(a/2) )^2}÷(2π)＝{(1/2)a^2-πa＋π^2}÷(2π)＝(1/(4π))a^2-(1/2)a+(1/2)π
a の値を (2/3)π からπ まで変化させたときの平均は、この f(a) を a で積分したものを (π/3) で割ればよい。
(1/(4π))a^2-(1/2)a+(1/2)π を ((2/3)π→π) で積分すると、
［(1/(12π))a^3-(1/4)a^2＋(1/2)πa］ ((2/3)π→π) ＝(7/81)π^2
よって、{(7/81)π^2}÷(π/3)＝(7/54)π　が求められた。

したがって、点Bが上半円のどこかに位置する（動径OBのなす角θが0からπの範囲にある）とき、3点A,B,Pがつくる最短の弧の長さは、上記2つの平均値（期待値）の和と考えられるので、(11/54)π＋(7/54)π＝(18/54)π＝π/3　となる。

円周上の2点がつくる弧の長さ

線分上の2点間の距離の考えを円周上に拡張してみる。

円周上にランダムに2点をとるとき、2点を結ぶ短い方の弧の長さはどれくらいか、を考える。

ランダムな2点がつくる弧の長さの平均を求めるということだ。

原点を中心とする単位円上において、片方の点Aを固定して、点Bを円周に沿って動かすとき、弧ABの長さは動径OBが回転した角度θに等しい。

短い方の弧を選ぶので、上半円のみで考えると、角度θが0からπまで変化するときの弧の長さθの平均値（期待値）を求めればよいので、

f(θ)＝θ の積分（0→π）を計算すると、［(1/2)θ^2］（0→π）＝(1/2)π^2

これを π－0＝π で割って平均をとると、θ＝π/2　となる。

これを図で表すと、青い図形の面積を底辺の長さで割ったものと考えられる。

つまり、円周上のランダムな2点がつくる弧の長さの平均は π/2 である。半円周は、その中点でバランスをとっている。

線分上のランダムな2点間の距離

標本が無限集合である例を考えていくのに、まずは次のような問題をとりあげる。

長さが1の線分上に、ランダムな2点をとるとき、2点間の距離（期待値）はどれくらいになるか、を考える。

数直線を0から1までで切り取った線分OAをについて、

第1点目の点をPとして、数直線上の適当な座標 x に位置づける。

（このとき、ランダムに置いた第1点の座標 x の平均は、1/2 になる。）

次に、第2点目の点をQとして、同じ線分OA上の適当なところに配置すると、PQ間の距離は次のようになる。

① QがOP上にあるとき、PQ間の距離は、0から x までの値をとる。

② QがPA上にあるとき、PQ間の距離は、0から 1-x までの値をとる。

点Qの移動によって、PQ間の距離の変化は次のように図示することができる。

つまり、点Pの座標を x としたとき、そのときのPQ間の距離の平均値（期待値）は、この青い部分の面積を底辺で割ったものになるので、

{(1/2)x^2＋(1/2)(1-x)^2}÷(1-0)＝x^2-x+1/2　となる。

ここで、点Pの座標 x が、0から1 までをランダムに変化すると考えて、

f(x)＝x^2-x+1/2　とおいて、f(x)を 0から1 まで積分して、全体の 1 で割れば、PQの一般的な距離の平均が求められるだろう。

つまり、先ほどと同様に、f(x)＝x^2-x+1/2 とx軸で挟まれた青い部分の面積を底辺で割ることで、高さ（PQ間の距離）の平均値（期待値）が算出できることになる。

すなわち、x^2-x+1/2（0→1）をxで積分して、

［(1/3)x^3-((1/2)x^2+(1/2)x］（0→1）＝1/3-1/2+1/2＝1/3　となる。

ベルトランのパラドックス（2）

円の中にランダムにひいた弦の長さが、内接する正三角形の一辺の長さａよりも長くなる確率について、次のような3つの意見に分かれたのだった。整理すると、

① Aさん
作業：円周上に適当な2点をとり、これを結んだものを「ランダムな弦」とする
比較対象：接線と弦のなす角（0°～180°）のうち、弦の長さがａよりも長くなる角度の範囲の割合を調べる
結果：確率は、60/180＝1/3

② Bさん
作業：1本の直径上に適当な点をとり、これを通り直径に垂直な線分を「ランダムな弦」とする
比較対象：直径上の点の位置（0～2ｒ）のうち、弦の長さがａよりも長くなる位置の範囲の割合を調べる
結果：確率は、r/2r＝1/2

③ Ｃさん
作業：円の内部に適当な点をとり、これが中点になるような線分（両端は円周上）を「ランダムな弦」とする
比較対象：円の内部（大円の面積）の点のうち、弦がａよりも長くなるような範囲（小円の面積）にある点の割合を調べる

結果：確率は、(π(r^2))/(4π(r^2))＝1/4

異なるアプローチは、異なる結果を導くことになった。
誰の解答が正しいのだろうか。正しくない解答があるとすれば、どこに誤りがあるのだろうか。解答に誤りがないとすれば、なぜこのような異なる結果が導かれるのだろうか。

実は、標本が無限集合である場合、確率を考える対象をどのように設定するかによって違いが現れることがある。
全事象の確率が 1 であること、互いに排反な事象のどれか一つでも起こる確率はそれらの確率の和によって決まること、という原則に則って、測ろうとする事象を明確に定める必要がある。（「確率測度」という。）

たとえば、問題文にある「円の中にランダムにひいた弦の長さ」という表現を、「円周上に適当な2点をとり、結んだ弦の長さ」と置き換えたなら、Aさんの答が正しいことになる。円周上の2点を角度θで表し、角θが0→πにおいて起こる確率を1とする可算空間を考えて、その確率を定義したわけだ。
もし、「円の直径上に適当な点をとり、これを通り直径に垂直な弦の長さ」と定めるなら、Bさんの答が正しくなる。この場合、直径上の点の位置をｘで表し、位置ｘが0→2rにおいて起こる確率を1としている。
さらに、「円の内部に適当な点をとり、これが中点になるような弦の長さ」と定めるなら、Cさんの答が正しくなる。この場合は、円の内部の点の集合全体を1としている。

ベルトランのパラドックスでは、弦の長さが内接正三角形の辺の長さよりも長くなる「確率」を扱っているが、標本が無限集合である場合の、線分の「長さ」（期待値）などについても、同じようなことが現れる。
引き続き、このような例を調べていきたい。

ベルトランのパラドックス（1）

下図は､円に内接する正三角形を描いたものである。この円の中にランダムに弦を引いたとき､その弦の長さが正三角形の一辺の長さ(ａ)よりも長くなる確率はいくらか、を考える。

適当に直線を引いたとき､円で切り取られた線分（弦）は、ℓ1のようにａより短いものや､ ℓ2のようにａより長いものが現れる。

このようにランダムに弦を引いたとき､その弦の総数に対して､ａよりも長くなる弦の本数の割合を求めようとしている。

Aさんは次のように考えた。

線を引くためのスタートになる点を円周上に設けて、この点から円の内部に線を引っ張っていく。

そうすれば、引いた線が三角形に重なるとき（線が赤色の角度内にあるとき） は、aより長く、三角形に重ならないとき (青色の角度内にあるとき) は､aより短くなり、これを区別すればよい。

ランダムに線を引ける角度は180度であるが、その内、赤い60度内に入れば、その線はaより長くなるといえる。

したがって、求める確率は､60/180＝1/3である。

Bさんは次のように考えた。

円の直径を1本引いて、この直径上にランダムに点をとる。この点を通り、直径に垂直な直線を円内に引いて、その線分の長さを比べればよい。

そうすれば、点が円の中心に近く、2つの正三角形の底辺に挟まれたところにあるとき（線が赤矢印内にあるとき）の線は、aより長く、その外側（中心から離れた青色の矢印内にあるとき） は、aより短くなる。

円の中心は正三角形の重心に位置するので、青色の矢印と赤色の矢印の長さは、上青：赤：下青＝1：2：1になる。

点のとり方はランダムなので、起こりやすさはこの長さの割合に等しいことから、求める確率は､2/4＝1/2 になる。

Cさんは次のように考えた。

円の中にランダムに点をとり、この点から直線を引く。さまざまな線の引き方が考えられるが、置いた点が中点となる弦（点を通り半径に垂直に引いた弦、点を通る最短の弦）をとることにする。

これは、Bさんが直径上の点をとって確かめたように、中心から直径の1/4（半径の1/2）の距離内にあるときに、aより長い線が引けることを意味する。

つまり、もとの大円の中にランダムな点をとるとき、その点が内側のオレンジの円の内部に存在する確率が、aより長い線が引ける確率ということになる。

よって、（小円の面積）/（大円の面積）＝π/4π＝1/4。

同じ問題を解いて異なる解答が現れるのは受け入れがたいということで、ベルトランの「パラドックス」と呼ばれている。

いろいろな平均（3）

④ 二乗平均平方根　√((a^2+b^2)/2)

台形ABCDの面積を等分するEFを定める。台形ABEF＝台形FECDなので、

BE＝kd、EC＝keとすると、(a＋c)×kd÷2＝(c＋b)×ke÷2より、d：e＝(b＋c)：(a＋c)

と表せることから、c＝a＋(bーa)×(b＋c)/(a＋b＋2c)　がいえる。

これを解くと、c^2＝(a^2＋b^2)/2、すなわち、c＝√((a^2+b^2)/2)　が導ける。

・d：e＝(b＋c)：(a＋c)

・一辺がそれぞれa､bの正方形の面積の和が、一辺cの正方形2つ分の面積に等しいということ。

・トイレットペーパーの真ん中を求める問題（以前に掲載）では、この二乗平均平方根を用いた。

全体の半径をa、芯の半径をbとしたとき、長いロールペーパーの真ん中付近までの半径（ある意味「平均」といえるだろう）をxとして、これを求めると、

π(x^2)ーπ(b^2)＝π(a^2)ーπ(x^2)　より、2(x^2)＝a^2＋b^2　すなわち、x＝√((a^2+b^2)/2)　となる。

（蛇足）このとき、下右図の2本の赤い接線の長さは等しくなる。

4つの「平均」をまとめてみると、

BE/ECは、それぞれ、① 1、② √a/√b、③ a/b、④ (b+c)/(a+c)　なので、

0＜a≦b　とすると、 ③ a/b ≦ ② √a/√b ≦ ① 1 ≦ ④ (b+c)/(a+c)　がいえる。

すなわち、点Eが点B側に近い順番は、③ 調和平均、② 相乗平均、① 相加平均、④ 二乗平均平方根　であり、その平均値（EFの長さ）も、③ 調和平均 ≦ ② 相乗平均 ≦ ① 相加平均 ≦ 二乗平均平方根　となる。

また、a=bのとき、すべてのEFの長さは等しく、a およびb に一致することがこれらの図から読みとれる。

さらに、① 相加平均 (a+b)/2、② 相乗平均 √(ab)、③ 調和平均 2ab/(a+b)　について、

((a+b)/2)×(2ab/(a+b))＝(√(ab))^2　が成り立つので、

2数の相乗平均は、「相加平均」と「調和平均」の「相乗平均」であることがわかる。

このことからも、③ 調和平均 ≦ ② 相乗平均 ≦ ① 相加平均　の関係が確かめられる。

 

いろいろな平均（2）

① 相加平均（Arithmetic mean）　M1=(a+b)/2

② 相乗平均（Geometric mean）　M2=√(ab)

③ 調和平均（Harmonic mean）　M3=2ab/(a+b)

④ 二乗平均平方根（root-mean-square）　M4＝√((a^2+b^2)/2)

これら4つの「平均」について、幾何学的な意味をもう少し深めてみよう。

AB＝a、DC＝b、AB∥DCの台形ABCD内に、

① (a+b)/2、② √(ab)、③ 2ab/(a+b)、④ √((a^2+b^2)/2)

の長さをもつ線分EFを引きたい。ただし、BC上にEを、AD上にFをとり、AB∥FEとなるように引くこととする。①～④は、それぞれどこに位置するか。

① 相加平均　(a+b)/2　について

BCの中点をEとする（d：e＝1：1）とき、c＝(a+b)/2　となる。

・EFは、ABとCDから等距離にある平行線。

・台形ABCEの面積＝BC×EF。

・a→c→bは、公差 (bーa)/2の等差数列。

② 相乗平均　√(ab)　について

台形ABEFと台形FECDが相似になるように点Eを定めると、

a：c＝c：b　となるので、c^2＝ab　すなわち、c＝√(ab)　になる。

・d：e＝√a：√b

・a→c→bは、公比 √(b/a) の等比数列。

・a､bを2辺とする長方形を裁ち合わせることによって、一辺cの正方形がつくれるということ。

③ 調和平均　2ab/(a+b)について

対角線ACとBDの交点Gを通り、ABに平行な直線FEを引くと、△AGB∽△CGDより、

BE：EC＝a：bなので、EF＝a＋(bーa)×a/(a＋b)＝2ab/(a＋b)

すなわち、c＝2ab/(a＋b)になる。

・d：e＝a：b

・aとbの逆数の平均がcの逆数になる、(1/a＋1/b)/2＝1/c　ということ。

・BCを一辺とする折り紙で、a､bの長さを定めると、a/(a＋b)の位置が導ける。

　（例：a＝1、b＝2のとき、辺の1/3の位置が求められる。）

いろいろな平均（1）

「平均」はいろいろな場面で使い分けが必要である。

 

① 相加平均（Arithmetic mean）

　M1＝(a+b)/2

　昨日の売り上げが2万円、今日の売り上げが6万円。2日間の平均売り上げはいくらか。

　(2+6)÷2＝4　4万円

② 相乗平均（Geometric mean）

　M2=√(ab)

　ここ2年間で年間売り上げが200万円から600万円に伸びた。2年間の平均伸び率と、平均伸び率から換算した昨年の売り上げはいくらか。

　√(600÷200)＝√3　√3倍　　200×√3≒346　346万円

　√(200×600)≒346　346万円

③ 調和平均（Harmonic mean）

　M3=2ab/(a+b)

　行きは時速20kmで、帰りは時速60kmで走った。往復の平均時速はいくらか。

　2x÷(x÷20＋x÷60)＝30　30km/h

　2×20×60÷(20+60)＝30　30km/h

④ 二乗平均平方根（root-mean-square）

　M4＝√((a^2+b^2)/2)

　一辺がそれぞれ2cmと6cmである正方形の板チョコ2枚を、一度溶かして同じ大きさの正方形の板チョコ2枚をつくるときその一辺（平均面積をもつ正方形の一辺）はいくらか。

　√((2^2+6^2)/2)≒4.47　4.47cm

2数a､bとこれら4つの平均値を幾何的に表現してみよう。

半円Oの直径AB上に、AC:CB＝a：bとなる点Cをとる。線分CD､OEはそれぞれABに垂直であるとする。

このとき、OEは半径なので、(a+b)の半分、すなわち、x＝(a+b)/2　…相加平均

△OCDは直角三角形なので、CD^2＝OD^2ーOC^2＝((a+b)/2)^2ー((b-a)/2)^2

＝(2ab+2ab)/4＝ab、すなわち、ｙ＝√ab　…相乗平均

△OCD∽CFDから、OD：DC＝CD：DFがいえるので、DF＝CD^2÷OD

＝ab÷((a+b)/2)＝2ab/(a+b)、すなわち、z＝2ab/(a+b)　…調和平均

△OCEも直角三角形なので、CE^2＝OC^2＋OE^2＝((a+b)/2)^2＋((b-a)/2)^2

＝2(a^2+b^2)/4＝(a^2+b^2)/2、すなわち、w＝√((a^2+b^2)/2)　…二乗平均平方根

ｚ≦ｙ≦ｘ≦ｗ（③ 調和平均 ≦ ② 相乗平均 ≦ ① 相加平均 ≦ 二乗平均平方根）であることが図から読み取れる。

また、点Cが点Oに重なるとき（a=bのとき）、ｚ＝ｙ＝ｘ＝ｗ　となる。

穴あき立方体の切断面（3）

 

『Autodesk Fusion 360』を使って、穴あき立方体の切断の3D画像をつくってみた。

このようなフリーツールが提供されていることはありがたい。

まずは、穴あき立方体の画像をつくるところから。

次に、面を指定してカットする。分けられた2つの立体をずらすと、その切断面が現れる。

② 正三角形

⑤ 長方形

⑥ 平行四辺形

⑦ 菱形

⑧ 台形

⑨ 等脚台形

⑩ 五角形

⑪ 六角形

⑫ 正六角形

以上、画像は10種類だけの紹介で終える。

実は、フリーで使うには制限があり、画像は10個までしか保存できない。

しかし、これだけ正確で、また自由度のある画像処理が、簡単な手順で行えるとは驚きである。