ランダムに引いた弦の長さ（6）

「円の中にランダムに引いた弦の長さ」について、また違った方法を考える。

（3）円の内部に適当な点をとり、その点が中点となるような弦の長さはどれくらいになるか。

⑤ 方法5

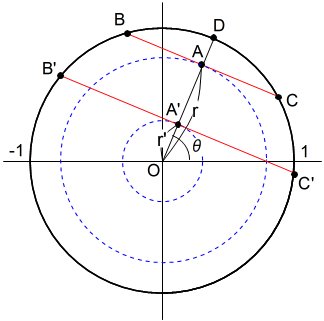
下図のように、中心が原点にある単位円の内部に適当な点Aをとり、OAに垂直な直線を引くとき、点Aを中点とする弦BCが引ける。円の内部にランダムな点をとった場合に、この弦BCの長さの平均を求めたい。

これまでとは異なり、点Aは2次元表記が必要になる。

点Aは、直交座標で、(x,y) （ただし、0≦ｘ≦1、0≦ｙ≦1、0≦x^2＋y^2≦1）と表す方法もあるし、

極座標で、(r,θ) （ただし、0≦ｒ≦1、0≦θ≦2π）と表す方法もある。ここでは極座標を用いて考える。

A(r,θ)を定めるとき、弦BCの長さは、2√(1－r^2) と表せる。θ は弦の長さには影響しない。

しかし、同じθ座標をもつOD上の点であっても、座標ｒが大きくなる（外周に近づく）と、その一周（点線）の長さが長くなることから、選ばれやすさも大きくなると思われる。

点Aと同じ半径ｒをもつ点の集まりは、2πrの長さの円周上の点であり、点A'と同じ半径r'をもつ点の集まりは、2πr'の長さの円周上の点であることから、点Aに対する点A'の選ばれやすさは、r'：r といえるだろう。

点Aよりも内側の点が選ばれる確率（πr^2/π）に対して、点A'より内側の点が選ばれる可能性（πr'^2/π）は、r'^2：r^2 、すなわち、半径の比（r'/r）の2乗に比例するという言い方もできる。