ランダムに引いた弦の長さ（2）

 

（1）円周上にランダムに2点をとるとき、2点間の距離はどれくらいになるか、の続き

③ 方法3

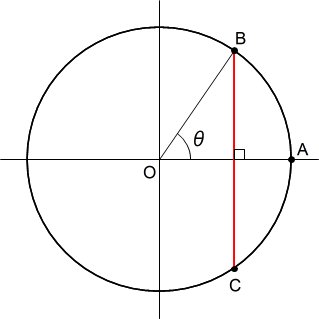
始線OAと動径OBのなす角をθとしつつ、弦の端点として点Aを使わずに、OAに垂直な線分BCによって、弦を定める。

この場合、ランダムとった2点としてはこれまで通り、A,B なのだが、A,B によって必然的に定められた点Cを用いて、BC間の距離を測るといった方法をとっている。

OB＝1より、BC＝2sinθと表せるので、前回の「② 方法2」と同じように、BCの長さについて、θ を 0→π/2 の範囲で積分して、π/2で割る作業を行う。

その平均値は、2÷(π/2)＝4/π　およそ、1.27　となる。

②と③を比べてみると、

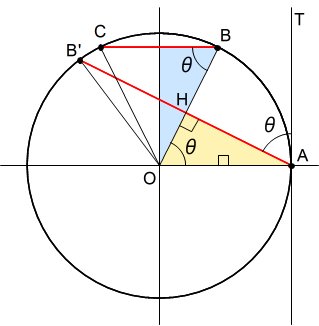
②において、接線と弦のなす角がθのとき、∠AOB'（＝2θ）の対辺AB'の長さを考えたが、これは、③における、∠BOC（＝2θ）の対辺、すなわちOAに垂直な線分BCの長さに相当することがわかる。

このように、円周上にランダムに2点をとるとした考え方だけでも、いくつかの方法があるのだが、基本的に、動径OBを回転運動させ、点Bの経路である半円周を「1」とした確率（期待値）を扱っているという点で共通である。

さらに、点Bに対して、y軸に垂直な弦をとるような設定もできる。この場合、BCはこれまでとは違って、AB'に一致しない。しかし、下図より、BC＝ 2cosθとなることから、θ を 0→π/2 で積分して、π/2で割れば、同じ結果が得られることがわかる。