線分上のランダムな2点間の距離

標本が無限集合である例を考えていくのに、まずは次のような問題をとりあげる。

長さが1の線分上に、ランダムな2点をとるとき、2点間の距離（期待値）はどれくらいになるか、を考える。

数直線を0から1までで切り取った線分OAをについて、

第1点目の点をPとして、数直線上の適当な座標 x に位置づける。

（このとき、ランダムに置いた第1点の座標 x の平均は、1/2 になる。）

次に、第2点目の点をQとして、同じ線分OA上の適当なところに配置すると、PQ間の距離は次のようになる。

① QがOP上にあるとき、PQ間の距離は、0から x までの値をとる。

② QがPA上にあるとき、PQ間の距離は、0から 1-x までの値をとる。

点Qの移動によって、PQ間の距離の変化は次のように図示することができる。

つまり、点Pの座標を x としたとき、そのときのPQ間の距離の平均値（期待値）は、この青い部分の面積を底辺で割ったものになるので、

{(1/2)x^2＋(1/2)(1-x)^2}÷(1-0)＝x^2-x+1/2　となる。

ここで、点Pの座標 x が、0から1 までをランダムに変化すると考えて、

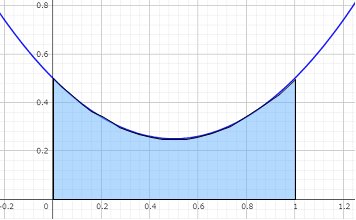
f(x)＝x^2-x+1/2　とおいて、f(x)を 0から1 まで積分して、全体の 1 で割れば、PQの一般的な距離の平均が求められるだろう。

つまり、先ほどと同様に、f(x)＝x^2-x+1/2 とx軸で挟まれた青い部分の面積を底辺で割ることで、高さ（PQ間の距離）の平均値（期待値）が算出できることになる。

すなわち、x^2-x+1/2（0→1）をxで積分して、

［(1/3)x^3-((1/2)x^2+(1/2)x］（0→1）＝1/3-1/2+1/2＝1/3　となる。