ビー玉を積む（2）

ビー玉の3層構造について、さらに考えてみよう。

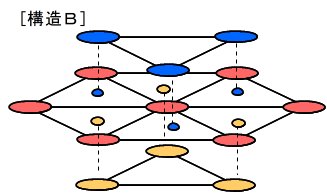
［構造A］と［構造B］について、下図のように、正六角形の配置と正三角形の配置の組み合わせで表現する（イラストは真横でなく少し上から見た感じ）。1層目の黄色（3個）、2層目の赤色（7個）、3層目の青色（3個）が、それぞれ下層の凹みに合うように積まれている。

［構造A］1層目と3層目が同じ位置にある構造。
　この構造に合わせてつくったビー玉のセットを「ブロックA」と呼ぶことにする。

［構造Ｂ］1層目と3層目が異なる位置にある構造。

　この構造に合わせてつくったビー玉のセットを「ブロックB」と呼ぶことにする。

ブロックＡとブロックＢの外側を覆う、なるだけ小さな多面体ケースをつくると（外側のビー玉がつくる共通接面をつなぐと）どんな立体が現れるだろうか。

どちらも、正三角形8枚と正方形6枚からなる十四面体になることが予想されたので、実際につくってみた。下の写真はそれぞれ、左側が［ブロックA］、右側が［ブロックＢ］である。

［ブロックＡ］［ブロックＢ］（のケース）はともに、同じ形・同じ数の面をもつ十四面体であり、どの頂点にも4面（正方形2面と正三角形2面）が集まる。ところが、辺（稜線）をつくる2面（隣り合う2面）の組合せが異なっている。［ブロックＡ］の場合、隣り合う2面は、正三角形同士、正方形同士、正三角形と正方形、の組が混在するが、［ブロックＢ］の場合は、正三角形と正方形が互いに隣り合い、同じ形が連続しない。

実は、上のような正三角形が4つ、正方形が3つ、（正六角形が1つ）からなる立体を「正三角台塔」と呼ぶのだが、［ブロックＡ］［ブロックＢ］（のケース）はどちらも、これを2個組み合わせたものになっている。［ブロックA］と［ブロックB］（のケース）の違いは、これを貼り合わせるとき、60度だけひねっているということだ。

［ブロックA］の立体は「同相双三角台塔」と呼ばれ、［ブロックB］の立体は「立方八面体」と呼ばれている。

紙でこの立体をつくってみて気づくことは、［ブロックB］はどの面を床に置いても上面が水平になる（向かい合う面がどれも平行）が、［ブロックA］は正三角台塔の真ん中の正三角形同士以外に互いに平行な面をもたないのだ。このことからも、ブロックBの方が高い対称性をもっているということがうかがえる。

「同相双三角台塔」（左）と「立方八面体」（右）の展開図は次の通り。