団子から考える（4）

双対多面体は、「面の重心を新たな頂点とし、辺で接する面の重心同士を辺で結び（したがって辺の数は変わらない）、頂点で接する面の重心を結ぶ多角形を面とする」（ウィキペディア）という。
確かめてみると、（昨日の写真で）左の立体の面の重心を結んで新たな多面体をイメージすると、右の立体の面の形、頂点に集まる面の数など、ちゃんと成り立っていることがわかる。頂点の数と面の数の入れ替わりも確認できる。

一つ、気になる点がある。
②体心立方格子について、ブロックの「菱形十二面体（頂点14、面12）」と団子の「切頂八面体（頂点24、面14）」では、「面12」と「頂点24」となっており、入れ替わりの数値が合っていないのだ。

ここで、「並べた団子をつぶす（2）」での発見を思い出したい。体心立方格子のブロック構造を調べたとき、初めは「四方六面体」（同じ二等辺三角形が24枚集まってできる二十四面体で、頂点14、面24をもつ）になると考えたが、結果的に「菱形十二面体」になったと説明した。菱形十二面体は、四方六面体の特殊な場合であると考えられる。ここで、フラットである菱形を2枚の二等辺三角形に分けて、その重心を点として結んでいくと、ちゃんと双対の関係が現れ、右側の立体（切頂八面体）の面の形・数が現れることがわかる。

・体心立方格子について

　ブロック構造：菱形十二面体（頂点14、面12）　四方六面体」（頂点14、面24）

　つぶれた団子：切頂八面体（頂点24、面14）

なぜ、このような美しい双対関係が表れるのだろうか。
「団子をつぶす」行為は、団子同士の縄張り争いと考えることができる。
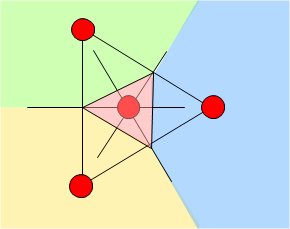
たとえば、平面上の3点に城を構えた3人の王がいて、それぞれの国の領土を主張したとする。城からの距離に偏りがでないように土地を分けようとすれば、下のような色分けで境界線を引くことになるだろう。

3点に囲まれた中央に、もう一人王がいた場合はどうだろう。それは、今回の「並んだ団子をつぶす」の条件に似ている。中央の領域は国でなくても、3つの王国の互いの中立地帯と考えてもいい。

全体の領土が3つの城がつくる三角形の内側だけに限られた場合は、こんな感じだろうか。

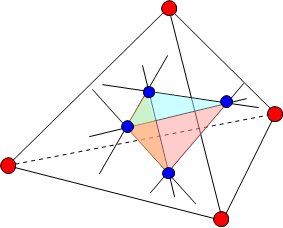
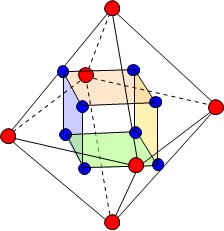
空間においても、ブロック構造の端にいる王が内部を取り合いつつ、中央に中立地帯を残すと考えてみよう。
たとえば、四面体の内部を4頂点にいる王たちが分割するならば、中央に上下逆さの四面体の形をした領域が現れるだろう。

また、たとえば、正八面体の内部を6頂点にいる王たちが分割するならば、立方体の領域が現れるだろう。

いずれの場合も、頂点の数（王の数）だけ、新しい領域の境界平面が現れることになる。

格子構造を調べる中で、偶然見つけた「双対」関係であったが、たまたまそうなったのではなく、このような理屈で必然のものであったといえる。また、「多面体の頂点と平面が入れ替わる」現象（結果）だけに注目するのでなく、そもそも「双対」とはどういう意味を持つのか、格子構造に照らして説明しようとする態度を大事にしたい。見方を変えれば、格子構造のブロック構造が分かれば、これに圧をかけたときの中央の球（団子）のつぶれ方が推測できるということである。もちろん、その逆を推測することも可能だ。

まだまだ、新たな疑問が湧いてきたり、不十分なところを補う必要があったりするのだが、ビー玉がらみの話題はこれで一区切りとしよう。