③[面心立方格子]の場合
面心立方格子の構造をビー玉を積んで表す方法は何通りか考えられる。
(a)5-4-5型
立方体の8頂点と6面に球を配置する面心立方格子の典型的な構造。(注目する球の周辺状況が分かりにくい。)
(b)4-5-4型
上記の「5-4-5型」の積み方を変えたもの。中央の赤い球に着目すると、上に4個、周囲に4個、下に4個の計12個の球に囲まれた(接した)構造になっている。
(c)3-7-3型
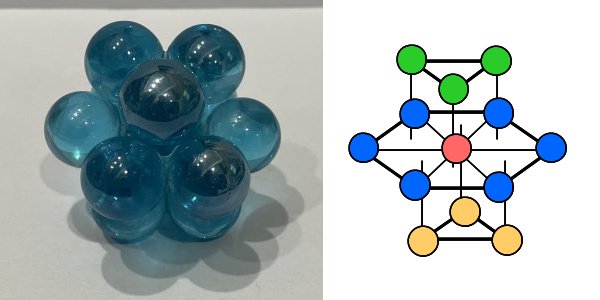
上記の「4-5-4型」を斜めに見たもの。(b)の右側のイラストと(c)のイラストを見比べると同じ構造であることがわかる。中央の赤い球に着目すると、上に3個、周囲に6個、下に3個の計12個の球に囲まれた(接した)構造になっている。
注目する赤い球が特殊な位置にある訳ではない。全ての球がこのような同じ周囲の条件を有しており、連続して配置されている。また、(a)も(b)も(c)も、一つの球に対して、12個の球が空間的に均等な方向に配置され、最密な状態で接している。
押しつぶした団子の形について、(c)の状態から考察してみると、周囲の青の球から圧迫された中央の球(赤色)は、側面を六角柱のように変形させられるだろう。これを上から3つの緑の球が押さえつけるので、とんがりの3面屋根が形成されるだろう。同様に、下から黄色の球がやはりとんがりの3面床(下に膨らむ)を形成すると考えられる。このとんがり屋根ととんがり床の3枚の面(菱形)の配置は、上下反対(60度回転対称ともいえる)で、全体として、バランスのとれたスタイルになると考えられる。
実は、この立体は「菱形十二面体」になる。
対角線が 1:√2の菱形12枚で構成され、3面が集まる頂点が8個、4面が集まる頂点が6個ある。上の写真は、それぞれ、<上から>、<下から>、<横から>、<4面がつくる頂点側から>見たものである。
菱形十二面体も一種類だけで空間を充填することができる立体である。
実際に、いくつかの菱形十二面体を積み重ねてみよう。正三角形(正六角形)、正方形などの積み重ねバリエーションが可能である。







0 件のコメント:
コメントを投稿