②［体心立方格子］の場合
体心立方格子構造に並んだ球をつぶす前に、体心立方格子の性質をもう少し調べておこう。
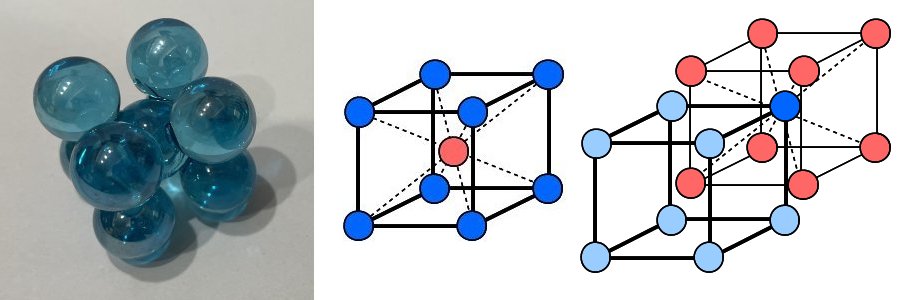
体心立方格子の基本形は、立方体の頂点と中心の計9つの球の配置であるが、実際にはこの構造が連続的に広がっている。2番目の写真は、基本形の上に1個追加したもの、3番目の写真は更に側面に4個追加したものである。
立方体の各面（4球の凹み）にビー玉がくっつくと、それは、面がピラミッド型の屋根をつけて膨らんだ立方体のようになる。これをブロックCと呼ぶことにする。
「ビー玉を積む（2）」でブロックAとブロックBの多面体ケースをつくったように、ブロックCのケースについても考えてみた。
おそらく「四方六面体」（立方体の各面の中心を持ち上げたような立体）になると想像し、そこに現れる二等辺三角形の形を考えた。
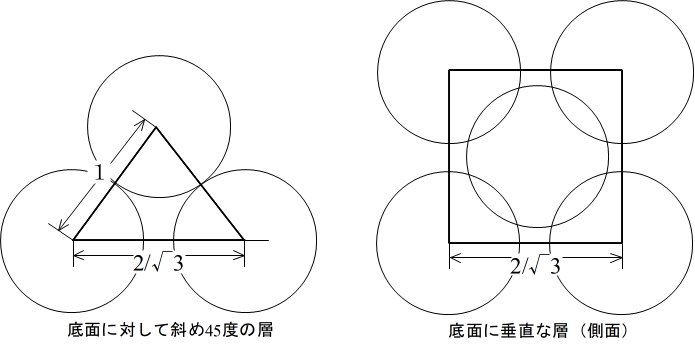
立方体の頂点に位置するビー玉の中心を図のように結ぶと1：√2：√3の直角三角形が描ける。注目したい二等辺三角形は、底辺を1とすると高さが(√2)/2になることが分かる。さっそく展開図を考えてつくってみた。
そして、新たな事実が発覚。
この展開図を組み立てたら、24枚の二等辺三角形による24面体ができると思っていたら、2面ずつがフラットな菱形をつくり、菱形十二面体になったのだ。
二等辺三角形をつくったときに気づくべきだった。対角線の比が 1：√2 になる菱形が12枚集まって多面体をつくるとき、菱形十二面体が形成されるのだから。（まあ、底辺1・高さ(√2)/2の二等辺三角形24枚で四方六面体はつくれない、ということがわかったことだけでも収穫としよう。）
つまり、体心立方格子構造は、菱形十二面体の対称性（立方体の対称性や正八面体の対称性など）をもつといえる。たとえば、向かい合わせの面は全て平行であり、見る角度によって正方形や正六角形が見える。
次に、体心立方格子の空間充填率を求めておこう。
前述の二等辺三角形の話から、ビー玉の直径を1としたとき、立方体の2頂点の距離は2/(√3)になる。一辺が2/(√3)の立方体の中に、全球が1個と8分の1球が8個が含まれるので、4/3×3.14×(1/2)＾3×2÷(2/(√3))^3≒1.047÷1.540≒.0.68＝68％
すでに調べた、面心立方格子や稠密六方格子の74％に比べると、やや隙間の多い構造といえる。
では、いよいよこの構造で配置された団子の圧縮を考えよう。
基本形における中央の球（赤色）に注目すると、8個の球に囲まれ、均等な8方向から圧を受けるので、正八面体の様相を形成することが予想される。しかし、この基本形は単独に存在するのでなく、中央の球はさらに6つの面の外側にある球からも圧を受けることになり、そこには立方体の要素が含まれる。また、見方を変えれば、各頂点の球（青色）は、基本形の中央の球でもあるのだ。全ての球が、立方体の8頂点方向からの圧と、同時に6面方向からの圧を受けることになる。では、その境界面（境界線）はどのようになるだろうか。
これを2次元に正確に描くのは困難だが、イメージとしては、菱形がカットされたり、正方形がカットされた、上のような赤枠の影をもつ立体になることが予想される。
正八面体の8枚の正三角形が、正八面体の6つの頂点付近でカットされ、そこに6枚の正方形の面をもつ立体。しかも、すべての球が同じ配置条件をもつので、圧縮された形状もすべて同一のものにならなければならない。このような形として、つぶれた団子は「切頂八面体」になると思われる。
「切頂八面体」は、正六角形が8枚、正方形が6枚の計14面からなる多面体である。見る方向によって、上記の予想した赤枠の影が現れている。
この切頂八面体は、一種類で空間を充填することができる。（隙間をなくすように圧縮したので当たり前だが。）
実際に、切頂八面体をいくつかつくって重ねてみた。
まずは、4個の球の凹みの上に1個の球が置かれた、基本的な構造が確認できる。
底面に対して斜め45度の層に注目してみると、正六角形状のきれいな連続模様が見られる。ただし、球をならべた際には正六角形ではなかった層であり、よく見ると、隣り合う接面には正六角形と正方形の2種類があることがわかる。
参考までに、切頂八面体の展開図は、次の通り。
また話が長くなってしまった。続きは明日へ。
0 件のコメント:
コメントを投稿