傾いた立方体の展開図（1）

6面が同じ形の菱形である「傾いた立方体」を考える。
向かい合う3組の面がそれぞれ平行（平行六面体）であり、かつ、一種類の菱形の面で構成される立体は「菱面体」と呼ばれている。工作用紙を切り貼りしてみると、次のような2個の異なる立体ができた。

各面の菱形は、短長の対角線の比が「1：√2」になるようにつくった。このとき、菱形の頂点の角はおよそ、70.5°と109.5°になる。（正四面体の二面角70.5°と正八面体の二面角109.5°がこんなところにも出てくる！）

①の立体は、約70°の角（鋭角）が3つ集まる頂点が2つあり、残りの6つの頂点には「1鋭角＋2鈍角」が集まる。
②の立体は、約110°の角（鈍角）が3つ集まる頂点が2つあり、残りの6つの頂点には「2鋭角＋1鈍角」が集まる。
このような菱形を組み合わせてつくる六面体は、この①と②の2種類の立体に限られる。
鈍角が120°以上の菱形でこのような立体をつくる場合は、一種類の立体しかつくれない。なぜなら、②のような3鈍角が集まる点は平面になるか重なってしまうから。

この菱面体の展開図をつくるには、①と②の立体で分けて考える必要がありそうだ。
また、立方体の展開図（11種類）に沿って考えることが漏れやだぶりを避けることになるだろう。
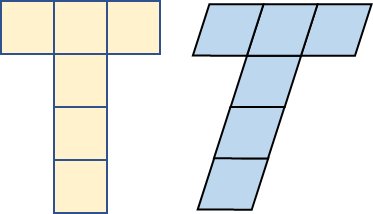
しかし、たとえば次のような「T字」の展開図について、正方形を単純に菱形に置き換えても上手くいかない。これでは、3鋭角（または3鈍角）の集まる頂点が存在しないのだ。

この展開図において、3面（青面）が集まる頂点（赤点）に注目するとき、①の立体を作るためには、3面の角が「3つの鋭角」か「1つの鋭角と2つの鈍角」になる必要がある。なお、このとき、同じくこの条件（「3つの鋭角」か「1つの鋭角と2つの鈍角」）から、残りの黄色の面のつなぎ方は必然的に決まる。

赤点に集まる3面の配置については、次の4つの場合が考えられるので、立方体の11種類の展開図に沿って、この4通りをあてはめて列挙していけばよいだろう。

なお、11種類の立方体の展開図において「注目する3面」については、次の通りとした。