傾いた立方体の展開図（3）

「菱面体」の展開図について、次に、「2つの頂点に菱形の3鈍角が集まる場合」（②の立体）を考える。

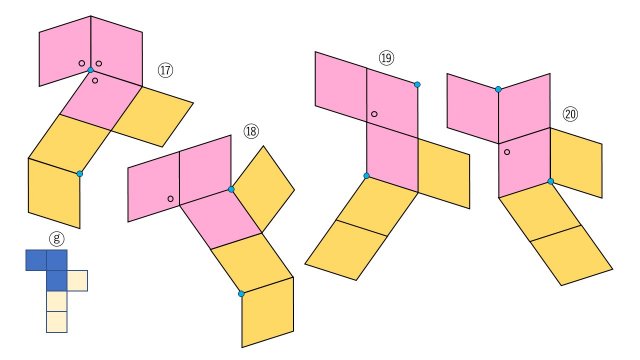
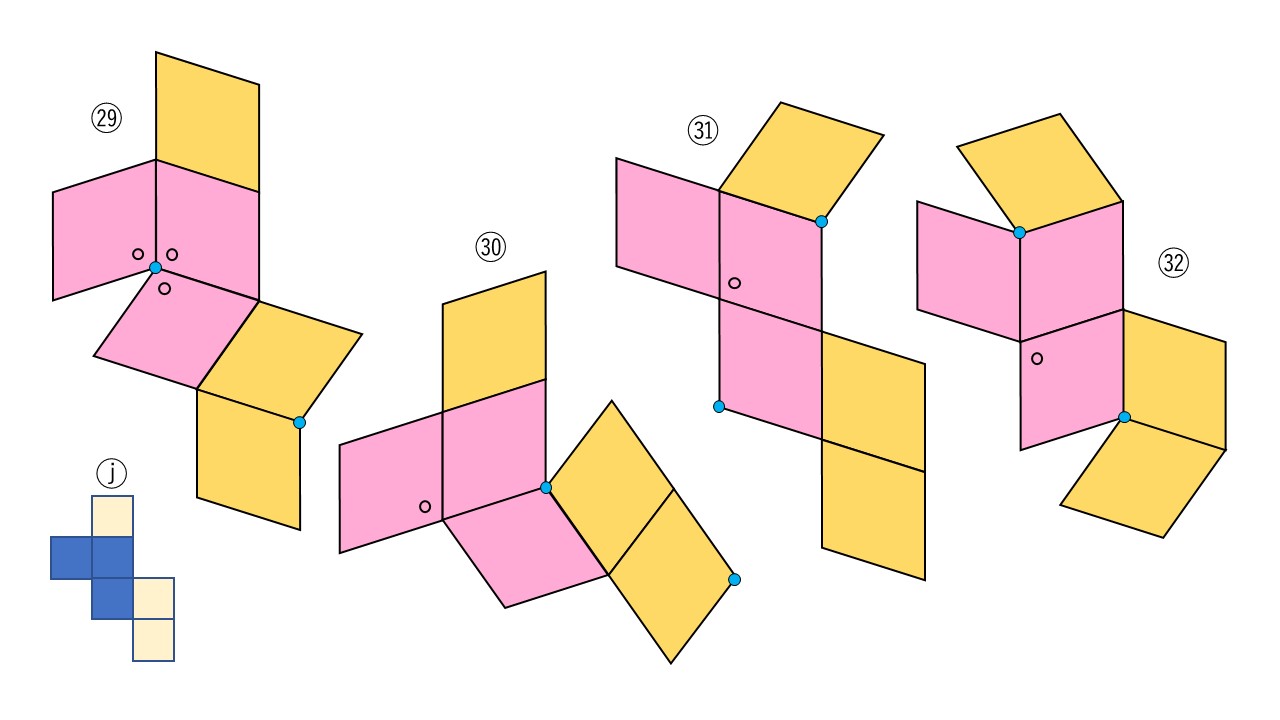
立方体の11種類の展開図における「注目する3面」については、前回（①の立体）と同様であるが、1点に集まる菱形の角については、「3つの鈍角」か「2つの鋭角と1つの鈍角」になる。すなわち、下図の青点に集まる3面の配置は、次のような4つのパターンに置き換えて考えることになる。なお、「注目する3面」以外の面のつなぎ方は必然的に決定される。

（a）型

（b）型

（c）型

（d）型

（e）型

（f）型

（g）型

（h）型

（i）型

（J）型

（k）型

2頂点に3鈍角が集まる菱面体（②の立体）の展開図の種類は、①の立体のものと同数であることがわかった。
繰り返しになるが、立方体の展開図が線対称である(a)(b)型については、裏返しをすることで同じになるものが2個ずつあり、点対称である(c)(d)(e)(f)型については、回転することで同じになるものが1個ずつ現れる。
したがって、11×4ー2×2－1×4＝36より、この立体（②）の展開図は全部で36種類ということになる。