(1)「折り紙」という作図
三角形の五心とは、内心、外心、垂心、重心、傍心の5つの心のことである。中学校では、コンパスと定規を用いてこれらを作図することを学ぶが、ここでは折り紙を使って考える。
折り紙の便利さに気づくとともに、作図の意味の振り返りができる。
折り紙の便利さに気づくとともに、作図の意味の振り返りができる。
(1)内心
<内心とは>
・三角形の内心とは、三角形の内部にぴったりと収まる内接円の中心である。
・つまり、内心は、3辺から等距離にある(内心から各辺に下した垂線の長さが等しい)。
・2辺から等距離にある点は、2辺をつくる角の二等分線上にあることから、次のような手順で作図できる。
<折り紙による内心の作図>
①辺ABと辺ACを重ねて折って、折り目をつける(∠Aの二等分線となる)。
②辺BAと辺BCを重ねて折って、折り目をつける(∠Bの二等分線となる)。
③2本の折り目が交わるところが、内心である。
(2)外心
<外心とは>
・三角形の外心とは、三角形の3頂点を通る外接円の中心である。
・つまり、外心は、3頂点から等距離にある。
・2頂点から等距離にある点は、2頂点を結ぶ線分(辺)の垂直二等分線上にあることから、次のような手順で作図できる。
<折り紙による外心の作図>
①点Aと点Bを重ねて折って、折り目をつける(辺ABの垂直二等分線になる)。
②点Bと点Cを重ねて折って、折り目をつける(辺BCの垂直二等分線になる)。
③2本の折り目が交わるところが、外心である。
<外心とは>
・三角形の外心とは、三角形の3頂点を通る外接円の中心である。
・つまり、外心は、3頂点から等距離にある。
・2頂点から等距離にある点は、2頂点を結ぶ線分(辺)の垂直二等分線上にあることから、次のような手順で作図できる。
<折り紙による外心の作図>
①点Aと点Bを重ねて折って、折り目をつける(辺ABの垂直二等分線になる)。
②点Bと点Cを重ねて折って、折り目をつける(辺BCの垂直二等分線になる)。
③2本の折り目が交わるところが、外心である。
(3)垂心
<垂心とは>
・三角形の垂心は、2つの頂点からそれぞれの対辺に下ろした垂線の交点をいう。したがって、次のような手順で作図できる。
<折り紙による垂心の作図>
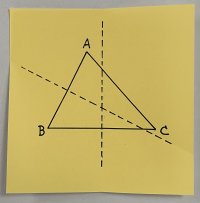
①点Aを折り目に含むように、その対辺(BC)を重ねて折る(Aから辺BCに下ろした垂線)。
<垂心とは>
・三角形の垂心は、2つの頂点からそれぞれの対辺に下ろした垂線の交点をいう。したがって、次のような手順で作図できる。
<折り紙による垂心の作図>
①点Aを折り目に含むように、その対辺(BC)を重ねて折る(Aから辺BCに下ろした垂線)。
②点Bを折り目に含むように、その対辺(AC)を重ねて折る(Bから辺CAに下ろした垂線)。
③2本の折り目が交わるところが、垂心である。
③2本の折り目が交わるところが、垂心である。
(4)重心
<重心とは>
・三角形の重心は、2つの頂点からそれぞれの対辺の中点を結ぶ直線の交点をいう。したがって、次のような手順で作図できる。
<折り紙による重心の作図>
①2点B,Cを重ねて折り中点に印をつけ、その中点と点Aを通る折り目をつける。
②2点C,Aを重ねて折り中点に印をつけ、その中点と点Bを通る折り目をつける。
③2本の折り目が交わるところが、重心である。
<重心とは>
・三角形の重心は、2つの頂点からそれぞれの対辺の中点を結ぶ直線の交点をいう。したがって、次のような手順で作図できる。
<折り紙による重心の作図>
①2点B,Cを重ねて折り中点に印をつけ、その中点と点Aを通る折り目をつける。
②2点C,Aを重ねて折り中点に印をつけ、その中点と点Bを通る折り目をつける。
③2本の折り目が交わるところが、重心である。
(5)傍心
・傍心は、三角形の外側にあり1辺と他の2辺の延長線に接する傍接円の中心のことであり、3つ存在する。3辺に接することから、各頂点の外角の二等分線が交わる点として作図できることがわかる。
・点I1と点Aを結んだ直線は、点I2と点I3を結んだ直線に直交し、かつ、∠BACを二等分する。
・すなわち、傍心は、2つの角の外角の二等分線と、残りの角の二等分線上にある。
・このことは、3つの傍心を頂点とする大三角形の垂心が、もとの三角形の内心に一致するということでもある。
・折り紙で作図する場合には、紙面の中央付近に三角形を3辺の延長線とともに描き、次のような手順で作図する。
<折り紙による傍心の作図>
・傍心は、三角形の外側にあり1辺と他の2辺の延長線に接する傍接円の中心のことであり、3つ存在する。3辺に接することから、各頂点の外角の二等分線が交わる点として作図できることがわかる。
・点I1と点Aを結んだ直線は、点I2と点I3を結んだ直線に直交し、かつ、∠BACを二等分する。
・すなわち、傍心は、2つの角の外角の二等分線と、残りの角の二等分線上にある。
・このことは、3つの傍心を頂点とする大三角形の垂心が、もとの三角形の内心に一致するということでもある。
・折り紙で作図する場合には、紙面の中央付近に三角形を3辺の延長線とともに描き、次のような手順で作図する。
<折り紙による傍心の作図>
①辺BAの延長線と辺ACを重ねて折って、折り目をつける(∠Aの外角の二等分線)。
②辺ABの延長線と辺BCを重ねて折って、折り目をつける(∠Bの外角の二等分線)。
③2本の折り目が交わるところが、傍心の一つになる。
②辺ABの延長線と辺BCを重ねて折って、折り目をつける(∠Bの外角の二等分線)。
③2本の折り目が交わるところが、傍心の一つになる。









0 件のコメント:
コメントを投稿