折り紙で模様づくり（4）

（4）創造性・独自性を磨く

折り紙で模様づくりを楽しむのに、厳密な方法の追求や証明は不要かもしれない。
でも、真面目な先生は、「学び方」を身につけてほしい、クリエイティブな人になってほしい、と願っている。だから、授業では「仕掛け」や「流れ」を大切にする。たとえば、「折り紙で模様づくり」のステップのように。

①予想する・やってみる（疑問をもって行動を起こす）
②振り返る・視野を広げる（数学的な要素を見つけてアプローチする）
③統合的・発展的に考える（学んだことを受けて自分の力を試す）
④創造性・独自性を磨く（自ら課題を見つけて新しい領域に挑戦する）

ちょっと無理矢理に小テーマをつけた感もあるけれど、①で終わってしまう授業はつまらない。①もやらずに、回転対称図形って簡単だよね、と済ます場合もあるかもしれないが。②では「対話的な学び」をイメージして問いかけを用意し、③ではオリジナリティを引き出すことを目指した。④は授業の中でなくてもOKで、自分で考える生徒が出てきたら大成功と考える。そのとき、誘い水になるような「窓」を見せるのは先生の仕事。

「10折り（5つ折り）ってどれもみんな近似値だよね。ネットで調べても正確な36°の折り方は見当たらなかった。挑戦しがいのある問題だと思うけど、折り紙の話はおしまいにして次の授業に行こうか。」なんて言われたら、チャレンジしようと思う生徒がでてくるかもしれない。

というわけで、正確な36°の10折り（5つ折り）で回転対称模様をつくる方法を考えてみた。

（f）辺の長さの比から36°の角度を導く方法

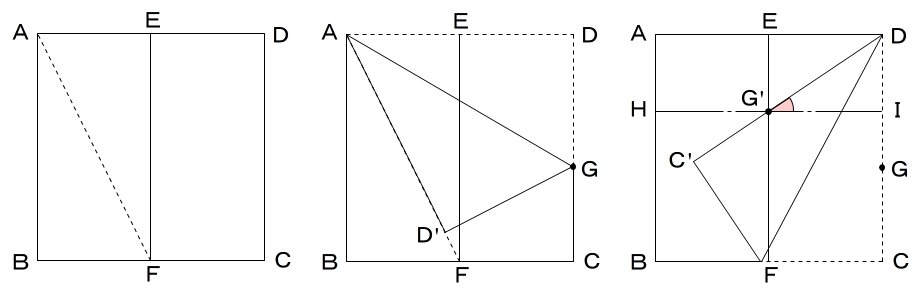
①折り紙をEFで半分に折り、更にAFを折る。
②折り目AFに辺ADを重ねたとき、辺CDの折れた点をGとする。
③点GがEF上に重なるように、辺DCを折ると、DG'と、ADに平行なHIのなす角が36°になる。

なぜ、これで36°が導けるのだろうか。

・AFの折り目をつけたとき、ここにできる△ABFは、1：2：√5の直角三角形である。
・ここで、正方形の一辺の長さを2としよう。　

・点DをD'に移動したとき、ここにできる△AJKと△GD'Kは合同で、また、1：2：√5の直角三角形になる。
・GD'の長さをxとおくと、JK＝x/2、KG＝(√5)x/2となり、JK＋KG＝2なので、
　(√5＋1)x＝4　　x＝4/(√5＋1)＝√5－1　となる。

・DG＝√5－1を、DG'に写しとったとき、そこにできる△DG'Iは、DG'：G'I＝(√5－1)：1になる。
・cosθ＝1/(√5－1)＝(1＋√5)/4　となるθは、正確に36°のときである。

＜確認＞
　θ＝36°＝π/5
　2θ＝πー3θ　とおいて
　sin 2θ＝sin(πー3θ)　を考える
　2 sinθ cosθ＝3 sinθー4 (sinθ)^3
　2 cosθ＝3ー4 (1ー(cosθ)^2)
　4 (cosθ)^2－2 cosθー1＝0
　cosθ＝(1±√(1＋4))/4　　cosθ＞0より　cosθ＝(1＋√5)/4　

この手順で折った折り紙で、回転対称の折り紙模様をつくってみた。

今の季節にぴったりだ。