折り紙で辺のｎ等分（2）

（2）辺の三等分の作図（その2）

［方法３］　重心の作図を利用する方法

「三角形の五心の作図」で確かめたように、重心は中線を 2:1 に内分する。これを使って、1/3 を導き出す方法を考えてみる。

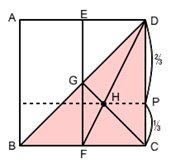
図のように、正方形ABCDを半分に折って、折り線BDとEFをつけ、その交点をGとする。次に、2点F、Dおよび2点C、Gを通る折り線を引き、その交点をHとするとき、点Hは△DBCの重心であり、DH:HF=2:1 が成り立つ。

すなわち、この点Hを通り辺ABに垂直な折り線で折るとき、図中の点Pは辺CDの3等分点の一つとなる。

［方法４］　正三角形を見出す方法

「正三角形の内心や外心は重心と一致する」ので、折り紙の中に正三角形を見いだせれば、1/3 を折るバリエーションが増える。

図のように、まず縦に二つ折りした折り線に点C’ が重なるように折り返す（操作⑤）と、△EBCができる。これは、下図でいえば、正三角形EBGの上半分と見ることができる。

（a）線分ECを折り線EBに重ねて折る（∠BECを二等分する／操作③）とき、その折り線がつくる辺BC上の点Fは、△EBGの内心かつ重心となるので、BCを三等分する。

（b）また、2点B、Eを重ねて折る（線分BEの垂直二等分線をひく／操作②）とき、その折り線がつくる辺BC上の点Fは、△EBGの外心かつ重心となるので、やはり、点Fは辺BCを三等分する。

［方法５］　芳賀の定理

辺の三等分については、芳賀の定理と呼ばれる3つの方法が知られている。更にこれを応用すると、辺の三等分だけでなく、任意の有理数分点を求めることが可能になる。

[1] 芳賀の第1定理

辺ADの中点をMとして、点C’ をこれに重ねて折り返す（操作②）とき、辺ABと辺B’C’ の交点Pは辺ABを三等分する。上図において、PB=1/3 AB

[2] 芳賀の 第2定理

辺ADの中点をMとし、BMを折り線として△MABを折り返す（操作①）。このときできる辺BA’に、辺BC’ を重ねて折る（操作③）とき、その折り線の端点Pは辺CDを三等分する。上図において、 CP=1/3 CD

[3] 芳賀の第3定理

辺ADの中点をMとして、辺A’B’が点Mを通り、かつ、点B’が辺CD上にあるように折り返す（操作⑤）とき、点B’は辺CDを三等分する。上図において、 CB'=1/3 CD