(5)a の立方根 ([3]√a)の作図
辺BC上に点E(1)、F(a) が与えられたとき、[3]√a (aの3乗根をこのように表すことにする)の長さを作図することを考える。
点Kを折り線IG上に、点Eを折り線LN上に重なるように折り返すとき、その折り線と、折り線HEの交点をP、折り線KMの交点をQとする。また、折り線HEとKMの交点をRとするとき、PRの長さは [3]√a となる。
なぜなら、PR=x とおくとき、
△MRP∽△PRQより、 1:x=x:RQ ∴ RQ=x^2
また、△PRQ∽△QREより、x:x^2=x^2:RE ∴ RE=x^3
ここで、RE=a なので、x^3=a x=[3]√a
すなわち、PR=[3]√a であることがわかる。
(6)角の三等分の作図(長さの作図ではないけど)
△MRP∽△PRQより、 1:x=x:RQ ∴ RQ=x^2
また、△PRQ∽△QREより、x:x^2=x^2:RE ∴ RE=x^3
ここで、RE=a なので、x^3=a x=[3]√a
すなわち、PR=[3]√a であることがわかる。
(6)角の三等分の作図(長さの作図ではないけど)
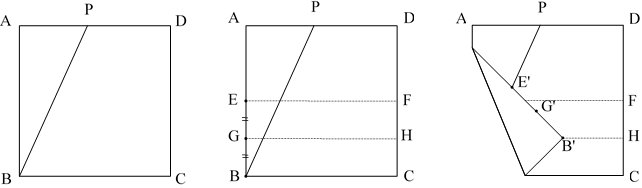
折り紙で作図シリーズの最後に、角の三等分の求め方を紹介しよう。
① 正方形ABCDを適当に折って、任意の∠PBCをつくる。
② BCに平行に2本の折り目EFとGHを、EG=GBとなるようにつける。
③ EがBP上に、BがGH上にくるように折り曲げ、E,Bが移った位置をE’,B’とする。
このとき、∠B’BC = 1/3 ∠PBCである。
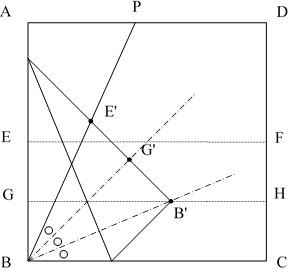
△IBB'、△JBB'、KBB'はいずれも二等辺三角形であることから、
∠IBJ=∠IB'J、∠JBB'=∠JB'B、∠KBB'=∠KB'B
一方で、
EG=GBより、∠EB'G(∠IB'J)=∠BB'G(∠BB'J)
GH∥BCより、∠GB'B(∠JB'B)=∠B'BK(∠KB'B)
したがって、∠E'BG'=∠G'BB'=∠B'BC がいえる。
∠IBJ=∠IB'J、∠JBB'=∠JB'B、∠KBB'=∠KB'B
一方で、
EG=GBより、∠EB'G(∠IB'J)=∠BB'G(∠BB'J)
GH∥BCより、∠GB'B(∠JB'B)=∠B'BK(∠KB'B)
したがって、∠E'BG'=∠G'BB'=∠B'BC がいえる。




0 件のコメント:
コメントを投稿