サイコロゲーム（2）

（2）サイコロAが他のサイコロと引き分ける理由

用意した正四面体のサイコロの目のパターンは次のようなものであった。

サイコロの目として用いた数は、

①（なるだけシンプルに）1～4の整数であること
②（不公平がでないように）目の合計を10にそろえること
を条件にしたものであった。
この条件下で考えられる目のパターンは、上記の他にもう一つ「2,2,3,3」（E型）というものが考えられるので、全部で5種類ということになる。
A型は、これらB,C,D,E型のいずれに対しても「6勝6敗4引き分け」になるのだが、その理由について考えてみたい。

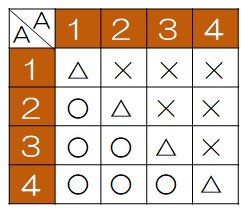
昨日の「引き分け」の対戦表をもう一度見てみると、

いずれの場合も「△」が4つ存在していることが分かる。まずは、その辺りから考えてみよう。

[1] 解説その1

サイコロAの相手が、A自身であったとすると、相手は1,2,3,4の目を一つずつもつので「△」が4つ存在する。また、表の中で、△の右は「×」、左は「○」になる。見方を変えると、表の中で、△の上は「×」、下は「○」といってもよい。△を境界にして、○が6つ、×が6つ存在している。
サイコロBとの対戦の場合、相手のサイコロを「1,2,3,4」（A）から「2,2,2,4」（B）に変更したと考える。目の和は10で変わらないので「1→2」と同時に「3→2」のように連動して目の数が変わる。このとき対戦表では、最も左の列の△が一つ下がって○が一つ減り、同時に左から3列目の△が一つ上がって○が一つ増える。つまり、△は4つのままで、○の数と×の数も6つずつが維持される。
同様に、「1,3,3,3」（C）は、「1,2,3,4」（A）を「2→3」「4→3」のように入れ替えたものであり、やはり「△」がずれることで、局所的に○、×の増減は生じるが相殺されることによって、全体としての△、○、×の数は変わらない。

「1,1,4,4」（D）もまた、「2→1」「3→4」の入れ替わりによって、「△」がずれるだけで、△、○、×の総数は変わらない。

△の移動による○と×の入れ替わりが必ずペアになって現れてくるのは、目の和を一定（10）にしたことによるものであり、どの対戦相手に対しても、A型vsA型の対戦と同様の結果（引き分け）を導くことになる。
したがって、△が4つ、○が6つ、×が6つという状態が常に維持される。
すなわち、サイコロAは、対戦相手によらず、必ず6勝6敗4分けで引き分けになる。

[2] 解説その2
もう少し一般的な説明（数式による表現）ができないだろうか。
相手のサイコロの4つの目を、a,b,c,dとするとき、1≦a,b,c,d≦4、a+b+c+d＝10である。
サイコロAは1から4の目を1つずつもっているので、相手のサイコロのa,b,c,dのうち、一つが「4」であるとき3つの「×」、「3」であるとき2つの「×」、「2」であるとき1つの「×」をもつことになる。つまり「目の数ー1」の負け数が見込まれる。つまり、負け数の合計は、(aー1)＋(bー1)＋(c－1)＋(d－1)＝a+b+c+d－4＝6　となることから、負け数は常に「6」になることがわかる。また、目の出方は全部で16通りあり、そのうち引き分けは必ず4通りあるので、×が6つ、△が4つ、○が6つとなる。
すなわち、サイコロAは、対戦相手によらず、必ず6勝6敗4分けで引き分けになる。

[3] 解説その3
別の数式によってこの現象を説明してみよう。
相手のサイコロの目について、「4」がp個、「3」がq個、「2」がr個、「1」がｓ個あるとすると、目の数の和が10であることから、4p+3q+2r+s＝10　･･･①　と表せる。
また、引き分けになるのは、p+q+r+s＝4　･･･②　の4通りある。
負ける（×がつく）のは、相手の「2」に対してｒ回、「3」に対して2q回、「4」に対しては3p回となるので、合計「3p+2q+r」回あるのだが、①ー②より、3p+2q+r＝6　が導けるので、負け数は「6」であることが分かる。
目の出方は16通り、引き分けは4通りなので、×が6つ、△が4つ、○が6つとなる。
すなわち、サイコロAは、対戦相手によらず、必ず6勝6敗4分けで、引き分けになる。

いろいろな説明の仕方ができるという点で、探究活動に相応しい教材であると思う。