折り紙で辺のｎ等分（1）

（1）辺の三等分の作図（その1）

折り紙の辺を三等分する方法を考えよう。
折り紙の作図の「操作②」や「操作③」（昨日の「基本形」の話）を使えば、辺の二等分や四等分は簡単にできる。しかし、辺を三等分、五等分するには、図形的な性質を使って工夫しなければならない。

［方法１］　辺の四等分から三等分を導く方法

図のように、四等分の折り目をつける。
点Dを折り目の端として、点C’ を線分EF上に置くと、辺C’Dを三等分する点が見つかる。
この方法を使えば、2^n 本の折り線を先につけておくことで、(2^n)ー1 以下の等分点を見出すことができる。

［方法２］　相似関係を見出す方法

折り線によって相似な三角形をつくり、相似比 1:2 から 1/3 を導き出す方法を考える（正方形の1辺の長さを1とする）。
図のように、正方形ABCDについて、対角線BD を折る。
次に、ADの中点Eを求め、2点E,Cを結ぶ折り線を引き、対角線との交点をGとする。
このときできる大小2つの三角形は、相似比 1:2 の相似形をなしている。つまり、DG:BG=1:2より、DG=1/3 DB である。

この点Gを通り辺ABに垂直な折り線で折るとき、図中の点Pは辺CDの三等分点の一つになる。また、点Gを通り辺BCに垂直な折り線で折るときも、図中の点Qは辺ADの三等分点の一つになる。

（応用１）

この三つ折りの方法は、紙幣などどんな長方形についても使える。
辺ADの中点Eをとり、折り線ECと対角線BDの交点をGとすると、この点Gを通り辺BCに垂直な直線PQが三つ折りの折り線になる。

（応用２）

コピー用紙（A4判やB5判）では、もっと簡単に三つ折りのポイントが見つけられる。
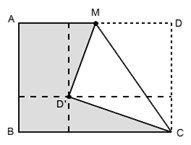
すなわち、図のように、辺ADの中点Mをとり、直線CMで折り返す（操作①）とき、点Dの移った点D’の位置は、長辺、短辺の両方にとって三等分点になっている。