折り紙で色々な長さ（2）

（3）a の平方根（√a）の作図

［方法1］

正方形ABCD の1辺の長さを a とし、辺BC上にBE＝1である点Eが与えられたとき、√a の長さを作図することを考える。
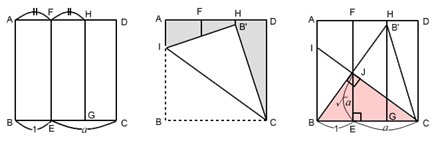
EC＝GEとなる点Gをとり、2点E、Gにおいて辺BCと垂直となる折り線FE、HGを引く。
点C’ がHG上に重なるように辺BC’ を折り返したときにできた折り線BIとCC’の交点をJとする。
このとき、△JBE∽△CBJより、BJ：1＝a：BJ 　BJ^2＝a 　∴ BJ＝√a である。

［方法2］

辺BCを 1：a に内分する点Eが与えられたとき、BE＝EG＝1となる点Gをとり、辺BCに垂直な折り線FE、HGを引く。

図のように、点B’ が折り線HG上に重なるように辺B’Cを折り返して点Iを定め、折り線ICとBB’の交点をJとする。
このとき、△BEJ∽△JECより、1：EJ＝JE：a　JE^2＝a　∴ JE＝√a である。

［方法3］

辺BCを 1：a に内分する点Eが与えられたとき、BE=EF=1となる点Fをとり、辺BCに垂直な折り線GFを引く。

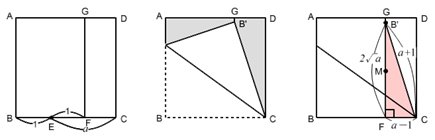
点B’ が折り線GF上に重なるように辺B’Cを折り返して点B’を定め、B’Fの中点Mをとると、MF＝√a となる。
なぜなら、△B’FCについて、FC＝aー1 　B'C＝a＋1  より、

B'F^2＝(a＋1)^2ー(aー1)^2＝4a　B'F=2√a　∴ MF=√a 。

［方法4］

辺BCを 1：a に内分する点Eが与えられたとき、点Eを通り辺BCに垂直な折り線FEを引き、辺BCの中点Gをとる。

点C’ が折り線FE上に重なるように点Gのところで折り返して点C’を定めるとき、C'E＝√a となる。
なぜなら、△C’EGについて、C'G=(a+1)/2、EG＝(a+1)/2ー1＝(aー1)/2  なので、

C'E^2＝((a＋1)/2)^2ー((aー1)/2)^2＝a　∴ C'E＝√a 。