正四面体がいっぱい（1）

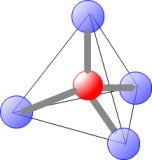
以前、ビー玉を積んだ構造を調べたとき、互いに接する3個のビー玉の上に1個のビー玉を乗せた構造が最も密で、安定することが分かった。自然界が好むと考えられるこのような形状を、正四面体構造と呼ぶ。

化学では、中央の原子の周りに、4個の別の原子が正四面体の頂点の位置に置かれる分子構造がよく見られ、四面体形分子構造と呼ぶ。例えば、中央に1個の炭素C、周りに4個の水素Hをもつメタン（CH4）などがある。

今回は、この正四面体、および、正四面体構造について考えてみよう。

（1）正六面体（立方体）を切る

正四面体も正六面体も、正多面体に属する。
正多面体とは、①面が1種類の正多角形からなる、②頂点に集まる面の数が同じ、③凸多面体である、という条件を満たす多面体のことで、正四面体、正六面体、正八面体、正十二面体、正二十面体の五種類しかない。
正多面体に関するさまざまな特徴については、書物やネット上に多く掲載されているので、ややマイナーなところ（生徒がたぶん知らないこと）を掘り下げていこう。

まず、正四面体、正六面体、正八面体について、面と面のなす角（二面角）を測ってみよう。
二面角とは、2つの面が作る交線に垂直な、2直線がなす角のことである。

生徒の測定結果は、正四面体が70°、正六面体が90°、正八面体が110°であった。
正確には、
　正四面体：70.5°
　正六面体：90°
　正八面体：109.5°　となる。
自分たちで測定した値は、聞いただけのときよりも記憶に残るだろう。

では、ここからが問題。
正六面体（立方体）の隣り合わない3頂点を選び、これを含む平面で切断するとき、三角錐（水色部分）はいくつ切り出せるか。また、切断して残った立体はどんな形か。

三角錐を切り出すとき、切り口は正三角形になる。その正三角形の頂点として利用する立方体の頂点は、下の図のように4つある（赤い点）。

立方体の残りの頂点4つが、三角錐の頂点部分にあたるので、水色の三角錐は4つ切り出せることが分かる。
では、切り取って残った立体はどんなものか。
切断面が同じ大きさの正三角形であること、その切断面が4面あることから、「正四面体」であることが推測される。

実際に、切って確かめてみよう。

立方体の発泡スチロールに、厚紙でつくったガードをあてて電熱カッターで切る。
途中経過も写真に収めたので紹介しよう。

三角錐を3個切り落とすところまでくると「正四面体」が見えてくる。
これら5つの立体を、真上から見たところ、斜め上から見たところは次の通り。

切断面は同じなので、上から見ると同じ大きさの正三角形が5つ並ぶが、切り取った三角錐と切り取られて残った三角錐（正四面体）とでは、高さが違っている。その高さの違いはちょうど2倍のようだ。「2倍」であることをどう確かめればよいか。

それぞれの高さを三平方の定理を使って計算で求めることもできるが、たとえば、こんな説明はどうだろう。
もとの立方体の一辺を1とすると、切り取った三角錐の体積は、(1/3)×(1/2)×1×1＝1/6で、これが4つあるので合わせて、4/6＝2/3になる。よって、残った三角錐（正四面体）は、1ー2/3＝1/3。底面の正三角形は同じ大きさの正三角形なので、それぞれの体積が、1/6と1/3 になるということは、高さの違いが「2倍」であるといえる。